题目内容
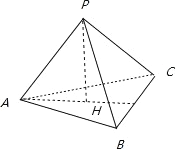
【题目】已知三棱锥
中，顶点
在底面的射影为
.给出下列命题：
①若
、
、
两两互相垂直，则为
的垂心；
②若、、两两互相垂直，则有可能为钝角三角形；
③若
，且与
重合，则三棱锥的各个面都是直角三角形；
④若，且为
边的中点，则
.
其中正确命题的序号是__________．（把你认为正确的序号都填上）
【答案】①③④
【解析】分析：利用线面垂直的判定与性质定理逐一判断即可.
详解：
若PA，PB，PC两两互相垂直，容易推出AH⊥BC，同理BH⊥AC，可得H是△ABC的垂心，①正确；
若
、
、
两两互相垂直，P在底面是射影H在△ABC的内部，是三角形ABC的垂心，所以不可能是钝角三角形，②不正确；
若
与
重合则PA⊥平面ABC，所以PA⊥AC，PA⊥AB，PA⊥BC，
又BC⊥AC，所以BC⊥平面PAC，所以BC⊥PC，
故四个面都是直角三角形，③正确；
当PH⊥平面ABC时，PA2=PH2+HA2，
PB2=PH2+BH2，PC2=PH2+CH2，
因为H是Rt△ABC斜边AB的中点，所以BH=AH=CH，
故PA=PB=PC，故④正确；
练习册系列答案
相关题目
