题目内容

用[x]表示不超过x的最大整数，如[0.75]=0，[3.01]=3．如果定义数列{x_n}的通项公式为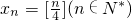 $数学公式$ ，则x₁+x₂+…+x_4n=________．

2n²-n
分析：先根据定义找到数列{x_n}的分布特点，进而求出其前4n项中数的分布，再代入求和公式即可．
解答：由题可得，数列{x_n}的各项为0，0，0，1，1，1，1，2，2，2，2，3，3，3，3，…
所以它的前4n项中，有3个0，4个1，4个2，…4个（n-1），一个n．
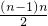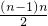故x₁+x₂+…+x_4n=4×1+4×2+4×3+…+4×（n-1）+n=4× $\text{[math]}$ +n=2n²-n．
故答案为2n²-n．
点评：本题是借助于[x]表示不超过x的最大整数，来考查等差数列的求和公式．是道基础题，关键点时理解新定义，并会用之来解题．

练习册系列答案

名师点拨中考导航系列答案

探究与训练系列答案

点知教育中考试卷汇编及详解系列答案

南通小题课时作业本系列答案

名师面对面同步课堂系列答案

精英口算卡系列答案

小学生每日10分钟系列答案

天利38套高中名校期中期末联考测试卷系列答案

口算题应用题天天练神机妙算系列答案

应用题点拨系列答案

相关题目

16、设x∈R，用[x]表示不超过x的最大整数，例如[-1.5]=-2，[5.1]=5、则下列对函数f（x）=[x]所具有的性质说法正确的有

．填上正确的编号）①定义域是R，值域是Z；②若x₁≤x₂，则[x₁]≤[x₂]；③[n+x]=n+[x]，其中n∈Z；④[x]≤x＜[x]+1．

（2013•青岛一模）定义区间（a，b），[a，b），（a，b]，[a，b]的长度均为d=b-a，多个区间并集的长度为各区间长度之和，例如，（1，2）∪[3，5）的长度d=（2-1）+（5-3）=3．用[x]表示不超过x的最大整数，记{x}=x-[x]，其中x∈R．设f（x）=[x]{x}，g（x）=x-1，当0≤x≤k时，不等式f（x）＜g（x）解集区间的长度为5，则k的值为（　　）

（2013•内江一模）定义区间（a，b），[a，b），（a，b][a，b]的长度均为d=b-a，多个区间并集的长度为各区间长度之和，例如（1，2）∪（3，5）的长度为d=（2-1）+（5-3）=3，用[x]表示不超过x的最大整数，记＜x＞=x-[x]，其中x∈R．设f（x）=[x]•＜x＞，g（x）=2x-[x]-2，若d₁，d₂，d₃分别表示不等式f（x）＞g（x）、方程f（x）=g（x）、不等式f（x）＜g（x）解集的长度，则当0≤x≤2012时，有（　　）

A．d₁=2，d₂=0，d₃=2010

B．d₁=1，d₂=1，d₃=2010

C．d₁=2，d₂=1，d₃=2009

D．d₁=2，d₂=2，d₃=2008

设x∈R，用[x]表示不超过x的最大值整数，则y=[x]称为高斯函数，下列关于高斯函数的说法正确的有

①[-x]=-[x]
②x-1＜[x]≤x
③?x，y∈R，[x]+[y]≤[x+y]
④?x≥0，y≥0，[xy]≤[x][y]
⑤离实数x最近的整数是-[-x+

定义区间（a，b），[a，b），（a，b]，[a，b]的长度均为d=b-a，多个区间并集的长度为各区间长度之和，例如，（1，2）∪[3，5）的长度d=（2-1）+（5-3）=3．用[x]表示不超过x的最大整数，记{x}=x-[x]，其中x∈R．设f（x）=[x]{x}，g（x）=x-1，当0≤x≤k时，不等式f（x）＜g（x）解集区间的长度为5，则k的值为（）
A．6
B．7
C．8
D．9