题目内容
19．若点P（-1，2）在角θ的终边上，则cosθ等于（ ）| A． | -2 | B． | $-\frac{{\sqrt{5}}}{5}$ | C． | $-\frac{1}{2}$ | D． | $\frac{2\sqrt{5}}{5}$ |
分析 首先求出P到原点的距离，然后利用三角函数的坐标法定义得到答案．
解答 解：因为点P（-1，2）在角θ的终边上，OP=$\sqrt{（-1）^{2}+{2}^{2}}=\sqrt{5}$，
所以cosθ=$\frac{-1}{\sqrt{5}}=-\frac{\sqrt{5}}{5}$；
故选B．
点评 本题考查了三角函数的坐标法定义；关键是明确利用角的终边上的点表示三角函数的方法．
练习册系列答案
相关题目
10．下列式子中成立的是（ ）
| A． | log0.44＜log0.46 | B． | 1.013.4＞1.013.5 | C． | 3.50.3＞3.40.3 | D． | log56＜log67 |
4．在△ABC中，b2cosC+bccosB=a2，则△ABC的形状是（ ）
| A． | 直角三角形 | B． | 锐角三角形 | C． | 等腰直角三角形 | D． | 等腰三角形 |
9．
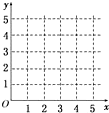某车间为了规定工时定额，需要确定加工零件所花费的时间，为此作了四次试验，得到的数据如下：
（1）在给定的坐标系中画出表中数据的散点图；
（2）求出y关于x的线性回归方程y=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$；
（3）试预测加工10个零件需要多少小时？（注：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$）
某车间为了规定工时定额，需要确定加工零件所花费的时间，为此作了四次试验，得到的数据如下：| 零件的个数x（个） | 2 | 3 | 4 | 5 |
| 加工的时间y（小时） | 2.5 | 3 | 4 | 4.5 |
（2）求出y关于x的线性回归方程y=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$；
（3）试预测加工10个零件需要多少小时？（注：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$）