题目内容
【题目】已知函数 ![]() ,当
,当 ![]() 时,函数
时,函数 ![]() 取得极值
取得极值 ![]() .
.
(Ⅰ)求函数 ![]() 的解析式;
的解析式;
(Ⅱ)若方程 ![]() 有3个不等的实数解,求实数
有3个不等的实数解,求实数 ![]() 的取值范围.
的取值范围.
【答案】解:(I) ![]() ,由题意:
,由题意: 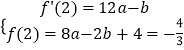 , 解得
, 解得 ![]() ,
, ![]() 所求的解析式为
所求的解析式为 ![]() .
.
(Ⅱ)由(1)可得 ![]() ,令
,令 ![]() ,得
,得 ![]() 或
或 ![]() ,
,
![]() 当
当 ![]() 时,
时, ![]() ,当
,当 ![]() 时,
时, ![]() ,当
,当 ![]() 时,
时, ![]() ,因此,当
,因此,当 ![]() 时,
时,
![]() 有极大值
有极大值 ![]() ,当
,当 ![]() 时,
时, ![]() 有极小值
有极小值 ![]() ,
, ![]() 函数
函数 ![]() 的图象大致如图.
的图象大致如图.
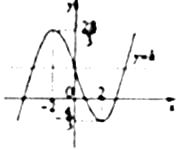
由图可知: ![]() .
.
【解析】(1)根据导数的意义,函数在某点有极值则该点的导函数的值为零,然后将x=2代入函数的解析式由此可得关于a与b的方程组,求解即可得出a与b的值,进而得到函数的解析式。(2)结合(1)中的结论,可得到函数的表达式根据导函数等于零求出函数的极值点,根据方程f ( x ) = k 有3个零点即可得到函数f(x) 与直线y=k有三个交点,根据题意作出函数的图像,进而得到k的取值范围。
【考点精析】认真审题,首先需要了解函数的极值与导数(求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值).
是极小值).

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
