题目内容
3．如果cosα=$\frac{1}{5}$，且α∈（-$\frac{π}{2}$，0），那么sinα=-$\frac{2\sqrt{6}}{5}$．分析 由条件利用同角三角函数的基本关系，以及三角函数在各个象限中的符号，求得sinα的值．
解答 解：cosα=$\frac{1}{5}$，且α∈（-$\frac{π}{2}$，0），那么sinα=-$\sqrt{{1-cos}^{2}α}$=-$\frac{2\sqrt{6}}{5}$，
故答案为：-$\frac{2\sqrt{6}}{5}$．
点评 本题主要考查同角三角函数的基本关系的应用，以及三角函数在各个象限中的符号，属于基础题．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
15．设f：A→B是从集合A到集合B的映射，则下列说法正确的是（ ）
| A． | A中不同元素的像必不同 | |
| B． | A中每一个元素在B中必有像 | |
| C． | B中每一个元素在A中必有原像 | |
| D． | B中每一个元素在A中必有唯一的原像 |
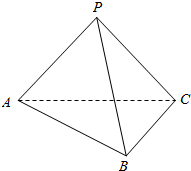如图，三棱锥P-ABC中，PA=PB=PC=AC=4，AB=BC=2$\sqrt{2}$．
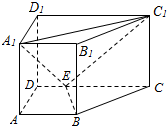如图，直四棱柱ABCD-A1B1C1D1中，AB∥CD，AD⊥AB，AB=2，AD=$\sqrt{2}$，AA1=3，E为CD上一点，DE=1，EC=3．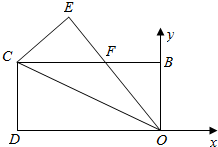
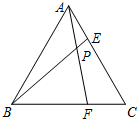等边三角形ABC的边长为6，在AC，BC边上各取一点E，F，连结AF，BE相交于点P．
15．若0＜x1＜x2，0＜y1＜y2，且x1+x2=y1+y2=1，则下列代数式中值最大的是（ ）
| A． | x1y1+x2y2 | B． | x1x2+y1y2 | C． | x1y2+x2y1 | D． | $\frac{1}{2}$ |
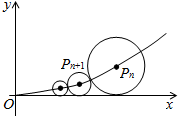在xOy平面上有一系列点P1（x1，y1），P2（x2，y2），…Pn（xn，yn）对每个正整数n，点Pn位于函数y=x2（x≥0）的图象上，以点Pn为圆心的圆Pn与H轴都相切，且圆Pn与圆Pn+1又彼此外切．若x1=1，且xn+1＜xn（n∈N+）．