题目内容
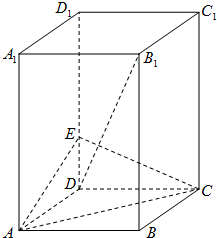 (2012•广州一模)如图,长方体ABCD-A1B1C1D1中,底面ABCD是正方形,AA1=2AB=2,E是DD1上的一点.
(2012•广州一模)如图,长方体ABCD-A1B1C1D1中,底面ABCD是正方形,AA1=2AB=2,E是DD1上的一点.(1)求证:AC⊥B1D;
(2)若B1D⊥平面ACE,求三棱锥A-CDE的体积;
(3)在(2)的条件下,求二面角D-AE-C的平面角的余弦值.
分析:(方法一)(1)证明AC⊥B1D,只需证明AC⊥平面BB1D;
(2)证明A1D⊥AE,求出DE=
,从而可求三棱锥A-CDE的体积;
(3)设A1D∩AE=F,AC∩BD=O,B1D∩OE=G,连接FG,证明∠DFG是二面角D-AE-C的平面角,由等面积关系求出DG,DF,从而可求二面角D-AE-C的平面角的余弦值.
(方法二)以D为原点,DA、DC、DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系
(1)证明
•
=0,可得
⊥
,从而AC⊥B1D;
(2)设E(0,0,a),利用B1D⊥平面ACE,可得
•
=0,从而可求体积;
(3)平面ADE的一个法向量为
=
=(0,1,0),面ACE的一个法向量为
=(1,1,2),利用向量的夹角公式,即可求二面角D-AE-C的平面角的余弦值.
(2)证明A1D⊥AE,求出DE=
| 1 |
| 2 |
(3)设A1D∩AE=F,AC∩BD=O,B1D∩OE=G,连接FG,证明∠DFG是二面角D-AE-C的平面角,由等面积关系求出DG,DF,从而可求二面角D-AE-C的平面角的余弦值.
(方法二)以D为原点,DA、DC、DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系
(1)证明
| DB1 |
| AC |
| DB1 |
| AC |
(2)设E(0,0,a),利用B1D⊥平面ACE,可得
| DB1 |
| AE |
(3)平面ADE的一个法向量为
| n1 |
| DC |
| DB1 |
解答: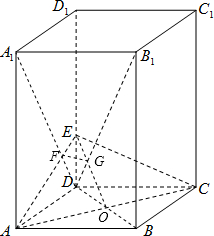 (方法一)(1)证明:连接AC,则AC⊥BD…(1分),
(方法一)(1)证明:连接AC,则AC⊥BD…(1分),
因为BB1⊥面ABCD,所以,BB1⊥AC…(2分),
因为BB1∩BD=B,所以AC⊥平面BB1D…(3分),
所以AC⊥B1D…(4分).
(2)解:连接A1D,与(1)同理可知A1D⊥AE…(6分),
从而
=
,DE=
…(7分),
所以VA-CDE=
×
×1×
×1=
…(8分)
(3)解:设A1D∩AE=F,AC∩BD=O,B1D∩OE=G,连接FG,
则AE⊥FG…(9分),所以∠DFG是二面角D-AE-C的平面角…(10分),
由等面积关系知DG=
=
…(11分),DF=
=
…(12分),
由(2)知∠DGF=
,sin∠DFG=
=
…(13分),
∴cos∠DFG=
…(14分).
(方法二)以D为原点,DA、DC、DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系…(1分).
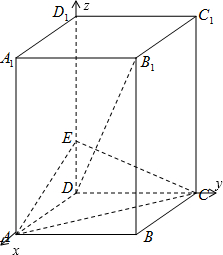 (1)证明:依题意,D(0,0,0),A(1,0,0),C(0,1,0),B1(1,1,2)…(3分),
(1)证明:依题意,D(0,0,0),A(1,0,0),C(0,1,0),B1(1,1,2)…(3分),
所以
=(-1,1,0),
=(1,1,2)…(4分),
所以
•
=0,
⊥
,所以AC⊥B1D…(5分).
(2)解:设E(0,0,a),则
=(-1,0,a)…(6分),
因为B1D⊥平面ACE,AE?平面ACE,所以B1D⊥AE…(7分),
所以
•
=0,所以-1+2a=0,a=
…(8分),所以VA-CDE=
×
×1×
×1=
…(9分)
(3)解:平面ADE的一个法向量为
=
=(0,1,0)…(10分),
平面ACE的一个法向量为
=(1,1,2)…(12分),
由图知,二面角D-AE-C的平面角的余弦值为cosθ=
=
=
…(14分).
 (方法一)(1)证明:连接AC,则AC⊥BD…(1分),
(方法一)(1)证明:连接AC,则AC⊥BD…(1分),因为BB1⊥面ABCD,所以,BB1⊥AC…(2分),
因为BB1∩BD=B,所以AC⊥平面BB1D…(3分),
所以AC⊥B1D…(4分).
(2)解:连接A1D,与(1)同理可知A1D⊥AE…(6分),
从而
| DE |
| AD |
| AD |
| AA1 |
| 1 |
| 2 |
所以VA-CDE=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 12 |
(3)解:设A1D∩AE=F,AC∩BD=O,B1D∩OE=G,连接FG,
则AE⊥FG…(9分),所以∠DFG是二面角D-AE-C的平面角…(10分),
由等面积关系知DG=
| DO×DE |
| OE |
| ||
|
| DA×DE |
| AE |
| 2 | ||
|
由(2)知∠DGF=
| π |
| 2 |
| DG |
| DF |
| ||
|
∴cos∠DFG=
| ||
| 6 |
(方法二)以D为原点,DA、DC、DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系…(1分).
 (1)证明:依题意,D(0,0,0),A(1,0,0),C(0,1,0),B1(1,1,2)…(3分),
(1)证明:依题意,D(0,0,0),A(1,0,0),C(0,1,0),B1(1,1,2)…(3分),所以
| AC |
| DB1 |
所以
| DB1 |
| AC |
| DB1 |
| AC |
(2)解:设E(0,0,a),则
| AE |
因为B1D⊥平面ACE,AE?平面ACE,所以B1D⊥AE…(7分),
所以
| DB1 |
| AE |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 12 |
(3)解:平面ADE的一个法向量为
| n1 |
| DC |
平面ACE的一个法向量为
| DB1 |
由图知,二面角D-AE-C的平面角的余弦值为cosθ=
| ||||
|
|
| 1 | ||
|
| ||
| 6 |
点评:本题考查线线垂直,考查三棱锥的条件,考查面面角,两法并举,注意体会.

练习册系列答案
相关题目
 (2012•广州一模)如图所示的茎叶图记录了甲、乙两个小组(每小组4人)在期末考试中的数学成绩.乙组记录中有一个数据模糊,无法确认,在图中以a表示.已知甲、乙两个小组的数学成绩的平均分相同.
(2012•广州一模)如图所示的茎叶图记录了甲、乙两个小组(每小组4人)在期末考试中的数学成绩.乙组记录中有一个数据模糊,无法确认,在图中以a表示.已知甲、乙两个小组的数学成绩的平均分相同.