题目内容
柜子里有3双不同的手套,随机地取出2只,试求下列事件的概率.(1)取出的手套不成对;
(2)取出的手套全是右手的;
(3)取出的手套全是同一只手的;
(4)取出的手套一只是右手的,一只是左手的,但它们不成对.
【答案】分析:(1)用间接法,从6只手套中任取2只共15种取法,手套成对的取法由3种,用1减去3除以15即可得到答案;
(2)用从3只右手手套任取2只得方法种数除以总种数15即可得到答案;
(3)取出的手套全是同一只手的概率等于全是左手和全是右手的概率和;
(4)可以先选出左手的一只有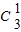 种选法,然后从剩下两双的右手中选出一只有
种选法,然后从剩下两双的右手中选出一只有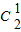 种选法,然后利用古典概型概率计算公式求解.
种选法,然后利用古典概型概率计算公式求解.
解答:解:(1)取出的手套不成对的概率p=1-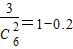 =0.8;
=0.8;
(2)取出的手套全是右手的概率p=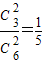 =0.2;
=0.2;
(3)取出的手套全是同一只手的概率等于全是左手和全是右手的概率和,即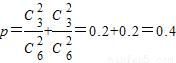 ;
;
(4)求取出的手套一只是右手的,一只是左手的,但它们不成对的概率,
可以先选出左手的一只有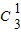 种选法,然后从剩下两双的右手中选出一只有
种选法,然后从剩下两双的右手中选出一只有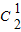 种选法,
种选法,
一共6种选法,故P=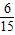 =0.4.
=0.4.
点评:本题考查了古典概型及其概率计算公式,解答的关键是在充分理解题意的基础上,求出基本事件个数,是基础题.
(2)用从3只右手手套任取2只得方法种数除以总种数15即可得到答案;
(3)取出的手套全是同一只手的概率等于全是左手和全是右手的概率和;
(4)可以先选出左手的一只有
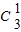 种选法,然后从剩下两双的右手中选出一只有
种选法,然后从剩下两双的右手中选出一只有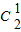 种选法,然后利用古典概型概率计算公式求解.
种选法,然后利用古典概型概率计算公式求解.解答:解:(1)取出的手套不成对的概率p=1-
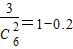 =0.8;
=0.8;(2)取出的手套全是右手的概率p=
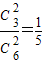 =0.2;
=0.2;(3)取出的手套全是同一只手的概率等于全是左手和全是右手的概率和,即
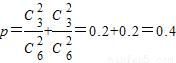 ;
;(4)求取出的手套一只是右手的,一只是左手的,但它们不成对的概率,
可以先选出左手的一只有
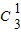 种选法,然后从剩下两双的右手中选出一只有
种选法,然后从剩下两双的右手中选出一只有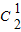 种选法,
种选法,一共6种选法,故P=
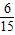 =0.4.
=0.4.点评:本题考查了古典概型及其概率计算公式,解答的关键是在充分理解题意的基础上,求出基本事件个数,是基础题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目