题目内容
已知x∈[0,1],函数f(x)=x2-ln(x+| 1 | 2 |
(Ⅰ)求函数f(x)的单调区间和值域;
(Ⅱ)设a≤-1,若?x1∈[0,1],总存在,使得g(x0)=f(x1)成立,求a的取值范围.
分析:(1)利用导数研究函数的单调区间的方法步骤求解f(x)的单调区间和值域.
(2)在a≤-1,x∈[0,1]的条件下,判断g(x)的单调性,进而求解g(x)的值域,依题意得f(x)的值域是g(x)值域的子集,列出关于a的不等式组,解出a的取值范围.
(2)在a≤-1,x∈[0,1]的条件下,判断g(x)的单调性,进而求解g(x)的值域,依题意得f(x)的值域是g(x)值域的子集,列出关于a的不等式组,解出a的取值范围.
解答:解:(Ⅰ)f/(x)=2x-
令f'(x)=0
解得:x=
,x=-1(舍去)
列表: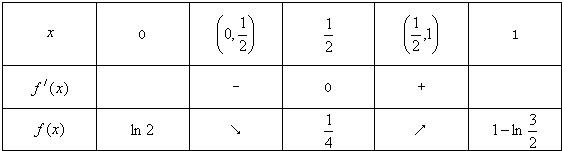
可知f(x)的单调减区间是(0,
),增区间是(
,1);
因为
<1-ln
=ln2-(ln3-1)<ln2,
所以当x∈[0,1]时,f(x)的值域为[
,ln2]
(Ⅱ)g′(x)=3(x2-a2)
因为a≤-1,x∈(0,1)
所以g′(x)<0,g(x)为[0,1]上的减函数,g(1)≤g(x)≤g(0)
所以g(x)∈[1-4a-3a2,-4a]
因为当x∈[0,1]时,f(x)的值域为[
,ln2]
由题意知:[
,ln2]⊆[1-4a-3a2,-4a]
所以
又a≤-1,得a≤-
.
| 1 | ||
x+
|
令f'(x)=0
解得:x=
| 1 |
| 2 |
列表:
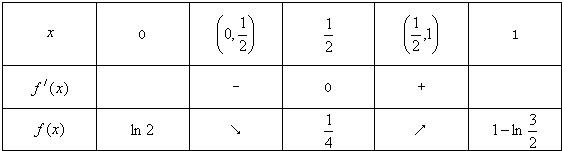
可知f(x)的单调减区间是(0,
| 1 |
| 2 |
| 1 |
| 2 |
因为
| 1 |
| 4 |
| 3 |
| 2 |
所以当x∈[0,1]时,f(x)的值域为[
| 1 |
| 4 |
(Ⅱ)g′(x)=3(x2-a2)
因为a≤-1,x∈(0,1)
所以g′(x)<0,g(x)为[0,1]上的减函数,g(1)≤g(x)≤g(0)
所以g(x)∈[1-4a-3a2,-4a]
因为当x∈[0,1]时,f(x)的值域为[
| 1 |
| 4 |
由题意知:[
| 1 |
| 4 |
所以
|
又a≤-1,得a≤-
| 3 |
| 2 |
点评:本题考查利用导数研究函数的单调性、值域等函数知识,对于(2)解答的关键是,f(x)的值域是g(x)的值域的子集,在学习中,同学们应熟练掌握这一方法,本题是一道好题,属于教学中的重点和难点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目