题目内容
【题目】已知椭圆![]() :
:![]()
![]() 的两个焦点为
的两个焦点为![]() ,
,![]() ,焦距为
,焦距为![]() ,直线
,直线![]() :
:![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,
两点,![]() 为弦
为弦![]() 的中点.
的中点.
(1)求椭圆的标准方程;
(2)若直线![]() :
:![]() 与椭圆
与椭圆![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() ,
,![]() ,若
,若![]() (
(![]() 为坐标原点),求
为坐标原点),求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]() 或
或![]()
【解析】
(1)因为![]() 为弦
为弦![]() 的中点,设
的中点,设![]() ,
,![]() ,将其代入
,将其代入![]() 利用点差法,即可求得答案.
利用点差法,即可求得答案.
(2)因为![]() ,
,![]() ,
,![]() 三点共线,
三点共线,![]() , 根据三点共线性质可得:
, 根据三点共线性质可得:![]() ,则
,则![]() ,将直线
,将直线![]() 和椭圆
和椭圆![]() 联立方程
联立方程![]() 消掉
消掉![]() ,结合已知,利用韦达定理即可求得答案.
,结合已知,利用韦达定理即可求得答案.
(1)![]() 焦距为
焦距为![]() ,则
,则![]() ,
,
设![]() ,
,![]() ,
,
![]()
![]() 为弦
为弦![]() 的中点,根据中点坐标公式可得:
的中点,根据中点坐标公式可得:![]() ,
,![]() ,
,
又![]() 将其
将其![]() ,
,![]() 代入椭圆
代入椭圆![]() :
:![]()
![]()

![]() 将两式作差可得:
将两式作差可得:![]() ,
,
![]()
 ,
,
![]()
![]() ——①.
——①.
![]()
![]() ——②
——②
由①②得: 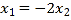
![]() 椭圆的标准方程为
椭圆的标准方程为![]() .
.
(2)![]()
![]() ,
,![]() ,
,![]() 三点共线,
三点共线,![]()
![]() 根据三点共线性质可得:
根据三点共线性质可得: ![]() ,则
,则![]()
设![]() ,
,![]() ,则
,则![]() ,
,
![]()
![]() .
.
将直线![]() 和椭圆
和椭圆![]() 联立方程
联立方程![]() 消掉
消掉![]() .
.
可得:![]() .
.
![]() ——①,
——①,
根据韦达定理:![]() ,
,![]() ,
,
代入![]() ,可得:
,可得:![]() ,
,![]() ,
,
![]()
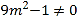 ,即
,即![]() .
.
![]()
![]() ,
,![]() ,
,
![]()
![]() ——②,
——②,
代入①式得![]() ,即
,即![]() ,
,
![]()
![]() ,
,
![]()
![]() 满足②式,
满足②式,
![]()
![]() 或
或![]() .
.

练习册系列答案
相关题目
【题目】空气质量指数![]() 是反映空气质量状况的指数,
是反映空气质量状况的指数,![]() 指数值越小,表明空气质量越好,其对应关系如表:
指数值越小,表明空气质量越好,其对应关系如表:
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
如图是某市10月1日—20日![]() 指数变化趋势:
指数变化趋势:
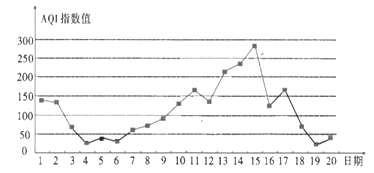
下列叙述正确的是( )
A.该市10月的前半个月的空气质量越来越好
B.这20天中的中度污染及以上的天数占![]()
C.这20天中![]() 指数值的中位数略高于100
指数值的中位数略高于100
D.总体来说,该市10月上旬的空气质量比中旬的空气质量差