题目内容
 如图,正方形ABCD所在平面与圆O所在平面相交于CD,线段CD为圆O的弦,AE垂直于圆O所在平面,垂足E是圆O上异于C、D的点,AE=3,
如图,正方形ABCD所在平面与圆O所在平面相交于CD,线段CD为圆O的弦,AE垂直于圆O所在平面,垂足E是圆O上异于C、D的点,AE=3,(1)求证:平面ABCD⊥平面ADE;
(2)已知二面角D-BC-E的平面角的正切值为
| ||
| 5 |
分析:(1)由已知中AE垂直于圆O所在平面,CD在圆O所在平面上,我们易得AE⊥CD,CD⊥AD,根据线面垂直的判定定理,易得CD⊥平面ADE,由面面平行的判定定理可得,平面ABCD⊥平面ADE.
(2)由已知中二面角D-BC-E的平面角的正切值为
,以D为坐标原点,分别以ED、CD所在的直线为x轴、y轴建立空间坐标系,利用向量法,易求出BE与平面ABCD所成的角的余弦值.
(2)由已知中二面角D-BC-E的平面角的正切值为
| ||
| 5 |
解答:解: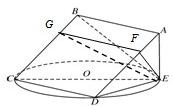 (1)证明:∵AE垂直于圆O所在平面,CD在圆O所在平面上,
(1)证明:∵AE垂直于圆O所在平面,CD在圆O所在平面上,
∴AE⊥CD.在正方形ABCD中,CD⊥AD,
∴CD⊥平面ADE.∴平面ABCD⊥平面ADE.(6分)
(2)以D为坐标原点,分别以ED、CD所在的直线为x轴、y轴
建立如图所示的空间直角坐标系,则D(0,0,0),E(-6,0,0),C(0,-3
,0),A(-6,0,3),B(-6,-3
,3).(8分)
设平面ABCD的法向量为n1=(1,0,2)向量.(9分)
设平面BCE的法向量为n2=(
,2,2
)(10分)
∴sin(
,
)=
.
∴cos(
,
)=
(13分)
故二面角D-BC-E的平面角的正切值为
.(14分)
 (1)证明:∵AE垂直于圆O所在平面,CD在圆O所在平面上,
(1)证明:∵AE垂直于圆O所在平面,CD在圆O所在平面上,∴AE⊥CD.在正方形ABCD中,CD⊥AD,
∴CD⊥平面ADE.∴平面ABCD⊥平面ADE.(6分)
(2)以D为坐标原点,分别以ED、CD所在的直线为x轴、y轴
建立如图所示的空间直角坐标系,则D(0,0,0),E(-6,0,0),C(0,-3
| 5 |
| 5 |
设平面ABCD的法向量为n1=(1,0,2)向量.(9分)
设平面BCE的法向量为n2=(
| 5 |
| 5 |
∴sin(
| n1 |
| n2 |
| 2 | ||
|
∴cos(
| n1 |
| n2 |
| 5 | ||
|
故二面角D-BC-E的平面角的正切值为
| 5 | ||
|
点评:本题考查的知识点是平面与平面垂直的判定,与二面角有关的立体几何综合题,用空间向量来解决二面角问题,其步骤是:建立空间直角坐标系?明确相关点的坐标?明确相关向量的坐标?通过空间向量的坐标运算求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB=
如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB= 8、如图把正方形ABCD沿对角线BD折成直二面角,对于下面结论:
8、如图把正方形ABCD沿对角线BD折成直二面角,对于下面结论: 如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<
如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a< 如图,正方形ABCD所在平面与等腰三角形EAD所在平面相交于AD,AE⊥平面CDE.
如图,正方形ABCD所在平面与等腰三角形EAD所在平面相交于AD,AE⊥平面CDE. (2010•温州二模)如图,正方形ABCD与正方形CDEF所成的二面角为60°,则直线EC与直线AD所成的角的余弦值为
(2010•温州二模)如图,正方形ABCD与正方形CDEF所成的二面角为60°,则直线EC与直线AD所成的角的余弦值为