题目内容
(理)已知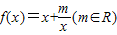 ,
,(1)若m≤2,求函数
 上的最小值;
上的最小值;(2)若函数
 在区间[1,+∞]上是减函数,求实数m的取值范围.
在区间[1,+∞]上是减函数,求实数m的取值范围.
【答案】分析:(1)先求导函数,根据m≤2,可分类讨论:若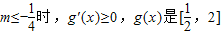 上的增函数,所以
上的增函数,所以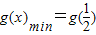 ;若
;若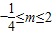 时,由g'(x)=0,得
时,由g'(x)=0,得 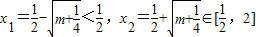
从而可知g(x)min=g(x2),故可求;
(2)由条件得到在区间上是增函数且f(x)+2>0在区间[1,+∞)上恒成立,利用分离参数法及函数的单调性可求实数m的取值范围.
解答:(理)解:(1)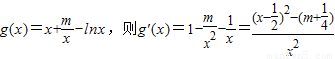
①若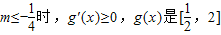 上的增函数,
上的增函数,
所以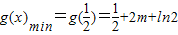 …(3分)
…(3分)
②若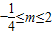 时,由g'(x)=0
时,由g'(x)=0
得到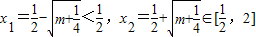
且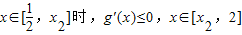 时,g'(x)≥0,
时,g'(x)≥0,
所以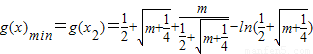 =
=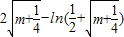 ;
;
…(6分)
(2)由条件得到在区间上是增函数且f(x)+2>0在区间[1,+∞)上恒成立,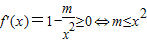 在区间上恒成立,得到m≤1,…(9分)f(x)+2≥0在区间上恒成立,得到f(1)+2>0,即m>-3,
在区间上恒成立,得到m≤1,…(9分)f(x)+2≥0在区间上恒成立,得到f(1)+2>0,即m>-3,
所以实数m的取值范围是:(-3,1]…(12分)
点评:本题以函数为载体,考查利用导数求函数的最值,考查函数的单调性,有一定的综合性.
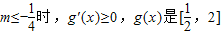 上的增函数,所以
上的增函数,所以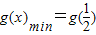 ;若
;若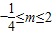 时,由g'(x)=0,得
时,由g'(x)=0,得 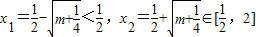
从而可知g(x)min=g(x2),故可求;
(2)由条件得到在区间上是增函数且f(x)+2>0在区间[1,+∞)上恒成立,利用分离参数法及函数的单调性可求实数m的取值范围.
解答:(理)解:(1)
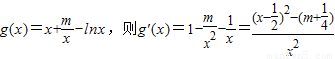
①若
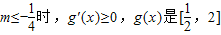 上的增函数,
上的增函数,所以
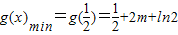 …(3分)
…(3分)②若
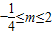 时,由g'(x)=0
时,由g'(x)=0得到
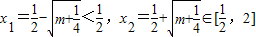
且
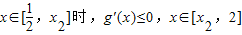 时,g'(x)≥0,
时,g'(x)≥0,所以
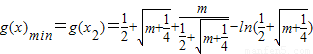 =
=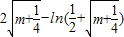 ;
; …(6分)
(2)由条件得到在区间上是增函数且f(x)+2>0在区间[1,+∞)上恒成立,
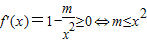 在区间上恒成立,得到m≤1,…(9分)f(x)+2≥0在区间上恒成立,得到f(1)+2>0,即m>-3,
在区间上恒成立,得到m≤1,…(9分)f(x)+2≥0在区间上恒成立,得到f(1)+2>0,即m>-3,所以实数m的取值范围是:(-3,1]…(12分)
点评:本题以函数为载体,考查利用导数求函数的最值,考查函数的单调性,有一定的综合性.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
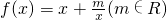 ,
,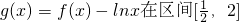 上的最小值;
上的最小值;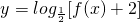 在区间[1,+∞]上是减函数,求实数m的取值范围.
在区间[1,+∞]上是减函数,求实数m的取值范围.