题目内容
（2013•徐州模拟）已知f（x）=log2（x-1），若实数m，n满足f（m）+f（n）=2，则mn的最小值是
9
9
．分析：由题目给出的函数解析式可以得到m和n均大于1，然后由f（m）+f（n）=2，得到mn-（m+n）=3．利用基本不等式转化为含mn的不等式，通过解不等式可以求得mn的最小值．
解答：解：由f（x）=log2（x-1），且实数m，n满足f（m）+f（n）=2，
所以log2（m-1）+log2（n-1）=2．
则
，
由①得（m-1）（n-1）=4，即mn-（m+n）=3．
所以3=mn-（m+n）≤mn-2
．
即mn-2
-3≥0．解得
≤-1，或
≥3．
因为m＞1，n＞1．所以
≥3，mn≥9．
故答案为9．
所以log2（m-1）+log2（n-1）=2．
则
|
由①得（m-1）（n-1）=4，即mn-（m+n）=3．
所以3=mn-（m+n）≤mn-2
| mn |
即mn-2
| mn |
| mn |
| mn |
因为m＞1，n＞1．所以
| mn |
故答案为9．
点评：本题考查了基本不等式，考查了利用基本不等式求最值，考查了对数函数的性质，利用了数学转化思想方法，是中档题．
练习册系列答案
相关题目
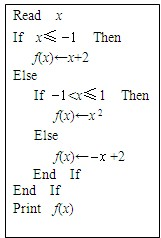（2013•徐州模拟）已知某算法的伪代码如图，根据伪代码，若函数g（x）=f（x）-m在R上有且只有两个零点，则实数m的取值范围是