题目内容
直三棱柱A1B1C1—ABC中,∠BCA=90°,点D1、F1分别是A1B1、A1C1的中点,BC=CA=CC1,则BD1与AF1所成的角的余弦值是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
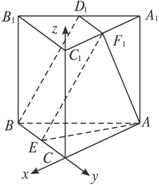
∵B1C1![]() BC,
BC,
∴D1F1![]()
![]() BC.
BC.
设点E为BC中点.
∴D1F1![]() BE.
BE.
∴BD1∥EF1.
∴∠EF1A或其补角为所求.
由余弦定理可求得cos∠EF1A=![]() .
.
答案:A

练习册系列答案
相关题目
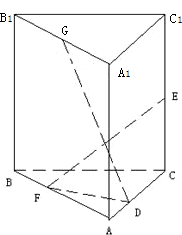 如图,在直三棱柱A1B1C1-ABC中,∠BAC=
如图,在直三棱柱A1B1C1-ABC中,∠BAC=| π |
| 2 |
A、[
| ||||||
B、[
| ||||||
C、[1,
| ||||||
D、[
|
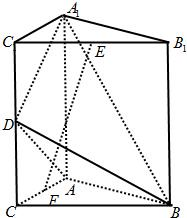 如图,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB. D、E分别为棱C1C、B1C1的中点.
如图,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB. D、E分别为棱C1C、B1C1的中点.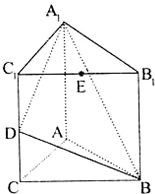 直三棱柱A1B1C1-ABC的三视图如图所示,D、E分别为棱CC1和B1C1的中点.
直三棱柱A1B1C1-ABC的三视图如图所示,D、E分别为棱CC1和B1C1的中点.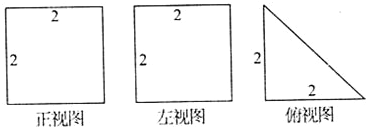
 如图,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB.D、E分别为棱C1C、B1C1的中点.
如图,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB.D、E分别为棱C1C、B1C1的中点.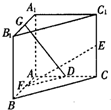 如图,在直三棱柱A1B1C1-ABC中,∠BAC=
如图,在直三棱柱A1B1C1-ABC中,∠BAC=