题目内容
选修4—5:不等式选讲
(1)已知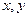 都是正实数,求证:
都是正实数,求证: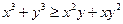 ;
;
(2)已知a,b,c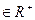 ,且a+b+c=1,求证:a2+b2+c2≥
,且a+b+c=1,求证:a2+b2+c2≥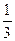 .
.
(1)已知
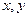 都是正实数,求证:
都是正实数,求证: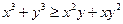 ;
;(2)已知a,b,c
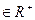 ,且a+b+c=1,求证:a2+b2+c2≥
,且a+b+c=1,求证:a2+b2+c2≥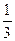 .
.(1)∵
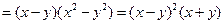 ,
,
又∵ ,∴
,∴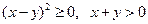 ,∴
,∴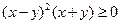 ,
,
∴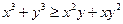 .…………………5分
.…………………5分
(2)由a+b+c="1," 得1=(a+b+c)2= a2+b2+c2+2ab+2bc+2ac≤3(a2+b2+c2)
∴a2+b2+c2≥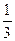 .(当且仅当a=b=c时取等号)…………………10分
.(当且仅当a=b=c时取等号)…………………10分

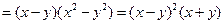 ,
,又∵
 ,∴
,∴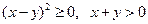 ,∴
,∴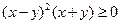 ,
,∴
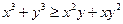 .…………………5分
.…………………5分(2)由a+b+c="1," 得1=(a+b+c)2= a2+b2+c2+2ab+2bc+2ac≤3(a2+b2+c2)
∴a2+b2+c2≥
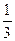 .(当且仅当a=b=c时取等号)…………………10分
.(当且仅当a=b=c时取等号)…………………10分略

练习册系列答案
相关题目

 的不等于
的不等于 的解集为空集,则实数
的解集为空集,则实数 的取值范围是
的取值范围是  .
. ,求不等式的解集;
,求不等式的解集;
 ,若不等式
,若不等式 在
在 上恒成立,则
上恒成立,则 的取值范围是( )
的取值范围是( )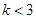



 , 求
, 求  的最大值和最小值.
的最大值和最小值.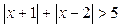 的解集为 .
的解集为 . 对任意的实数
对任意的实数 恒成立,则实数
恒成立,则实数 的取值范围是 .
的取值范围是 .