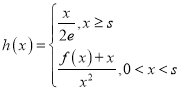Question

【题目】若椭圆的顶点和焦点中，存在不共线的三点恰为菱形的中心和顶点，则的离心率等于（ ）

A.B.C.或D.或

Answer 1

【答案】D

【解析】

由菱形对角线互相垂直可转化为，在椭圆的顶点和焦点中找到不共线的三点能构成一个直角三角形，结合椭圆的对称性，只须考虑三种情况，作出图形，从而求得椭圆的离心率.

依题意，由菱形对角线互相垂直可转化为，在椭圆的顶点和焦点中找到不共线的三点能构成一个直角三角形，结合椭圆的对称性，只须考虑三种情况：

（1）如图1，若以顶点焦点为菱形顶点，为中心，则，由勾股定理得，，由化简得，

两边同除以，得，又因为，可得．

（2）如图2，若以焦点,为菱形顶点，为中心，则，故，易得；

（3）如图3，若以焦点为菱形的中心，,为顶点，则，易得，故选D.