题目内容
已知椭圆
+
=1(a＞b＞0)内有一点A,F1为左焦点,F2为右焦点,在椭圆上求一点P,使|PF1|+|PA|取得最值.
思路解析：求曲线上一动点与某定点距离之和的最值,往往是利用几何变换,使得P、F1、A三点共线，或构建三角形，利用三角形的性质确定大小，进而确定最值的. 解：如图，设AF2与椭圆交于P1、P2两点，点M是椭圆上不同于P1、P2的任意一点. 根据椭圆的定义,得|P1F1|+|P1F2|=2a, ∴|P1F1|+|P1A|=|P1F1|+|P1F2|+|F2A|=2a+|F2A|. 在△AMF2中，|MA|＜|MF2|+|F2A|， ∴|MF1|+|MA|＜|MF1|+|MF2|+|F2A|=2a+|F2A|. ∵点M是椭圆上任意一点，∴|MF1|+|MA|＜2a+|F2A|, ∴|MF1|+|MA|＜|P1F1|+|P1A|. 点P1是使|PF1|+|PA|取得最大值的点. 同理,|P2F1|+|P2A|=|P2F1|+|P2F2|-|AF2|=2a-|AF2|. 在△AMF2中，|MA|＞|MF2|-|AF2|. ∴|MF1|+|MA|＞|MF1|+|MF2|-|AF2|=2a-|AF2|. ∴|MF1|+|MA|＞|P2F1|+|P2A|. ∴点P2是使|PF1|+|PA|取得最小值的点.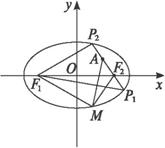
王朝霞小升初重点校系列答案
专项卷和真题卷系列答案
文曲星中考总复习系列答案
问题引领系列答案
先锋题典系列答案
知识大集结系列答案
随堂口算系列答案
小学升学夺冠系列答案
培优好题系列答案
培优60课系列答案
=1(a＞b＞0)的左焦点到右准线的距离为
,中心到准线的距离为
，则椭圆的方程为 
+y2=1 B.
+y2=1
=1 D.
=1
=1(a＞b＞0)的两个焦点为F1、F2，过F2作垂直于x轴的直线与椭圆相交，一个交点为P，若∠PF1F2=30°，那么椭圆的离心率是（ ）
=1(a＞b＞0)与双曲线
=1(m＞0,n＞0)有相同的焦点(-c，0)和(c，0)，若c是a、m的等比中项，n2是2m2与c2的等差中项，则椭圆的离心率是( )
B.
C.
D.
=1(a＞b＞0)的离心率为
，直线y=
x+1与椭圆相交于A、B两点，点M在椭圆上，
=
+
，求椭圆的方程.
=1(a>b>0)与x轴的正半轴交于点A,O是原点.若椭圆上存在一点M,使MA⊥MO,求椭圆离心率e的取值范围.