题目内容
(本小题满分12分)
已知数列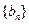 满足
满足 ,且
,且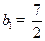 ,
,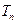 为
为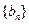 的前
的前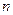 项和.
项和.
(Ⅰ)求证:数列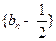 是等比数列,并求
是等比数列,并求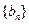 的通项公式;
的通项公式;
(Ⅱ)如果对任意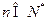 ,不等式
,不等式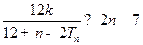 恒成立,求实数
恒成立,求实数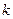 的取值范围.
的取值范围.
解:(Ⅰ)对任意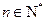 ,都有
,都有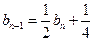 ,所以
,所以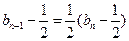
则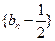 成等比数列,首项为
成等比数列,首项为 ,公比为
,公比为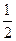 …………2分
…………2分
所以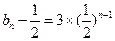 ,
, …………4分
…………4分
(Ⅱ)因为
所以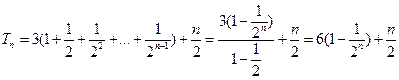 …………6分
…………6分
因为不等式 ,化简得
,化简得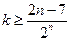 对任意
对任意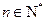 恒成立…………7分
恒成立…………7分
设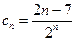 ,则
,则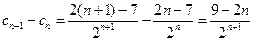 …………8分
…………8分
当 ,
,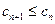 ,
,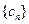 为单调递减数列,当
为单调递减数列,当 ,
,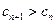 ,
,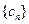 为单调递增数列
为单调递增数列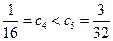 ,所以,
,所以, 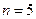 时,
时,  取得最大值
取得最大值 …………11分
…………11分
所以, 要使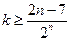 对任意
对任意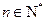 恒成立,
恒成立,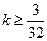 …………12分
…………12分
解析

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目