题目内容
给出下列四个命题：
（1）在△ABC中，内角A,B,C的对边分别为a,b,c,且
，则
;
（2）设
是两个非零向量且
，则存在实数λ，使得
；
（3）方程
在实数范围内的解有且仅有一个；
（4）
；
其中正确的个数有
| A．4个 | B．3个 | C．2个 | D．1个 |
A
解析试题分析：由正弦定理可得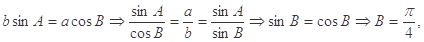
所以（1）正确；由可知两个向量共线，所以，所以（2）正确；分别画出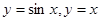
的图象可知，两个函数图象只有一个交点，所以（3）正确；
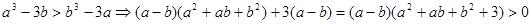恒成立，所以
，所以（4）也正确.
考点：本小题主要考查正弦定理的应用，向量共线的判断和应用，函数零点个数的判断和不等式性质的应用，考查学生灵活运用所学知识解决问题的能力.
点评：此种问题类似多项选择题，要灵活运用所学知识，仔细分析问题解决问题.
练习册系列答案
名师点拨卷系列答案
相关题目
在△ABC中，若
，则B的值为（ ）
| A．30° | B．45° | C．60° | D．90° |
的左右焦点，顶点P在双曲线C上，则
得值等于（ ）
(B) 
(C) 
(D) 
在
中，若
，则
的值为( )
A． | B． | C． | D． |
中，
,
,则
A． | B． | C． | D． |
已知
中，
所对的边分别为
，且
,那么角
等于( )
A． | B． | C． | D． |
在斜三角形ABC中，
，且
，则
的值为 （ ）
A． | B． | C． | D． |
已知△
中，
，则△ABC一定是
| A．等边三角形 | B．等腰三角形 |
| C．直角三角形 | D．等腰直角三角形 |
在△ABC中，C＝60°，AB＝
，BC＝
，那么A等于( )．
| A．135° | B．105° | C．45° | D．75° |