题目内容
 中,
中, ,
, ,则
,则
A. | B. | C. | D. |
C
解析试题分析:由正弦定理可得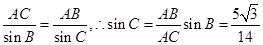 ,根据同角三角函数的基本关系式可知
,根据同角三角函数的基本关系式可知
 .
.
考点:本小题主要考查正弦定理和余弦定理,同角三角函数的基本关系式.
点评:解决此题也可以用余弦定理先求出第三条边,再依赖余弦定理求出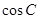 .解决此类问题,关键是灵活应用正弦定理和余弦定理,还要注意解的个数问题.
.解决此类问题,关键是灵活应用正弦定理和余弦定理,还要注意解的个数问题.

练习册系列答案
相关题目
若△ABC能被一条直线分成两个与自身相似的三角形,那么这个三角形的形状是( )
| A.钝角三角形 | B.直角三角形 |
| C.锐角三角形 | D.不能确定 |
三角形两条边长分别为2和3,其夹角的余弦值是方程2 -3x+1=0的根,则此三角形周长为
-3x+1=0的根,则此三角形周长为
A. | B.7 | C.5+ | D.5+2 |
如图,在地面 处测得树梢的仰角为60°,
处测得树梢的仰角为60°, 与树底部
与树底部 相距为5米,则树高为( )
相距为5米,则树高为( )
A. 米 米 | B.5米 | C.10米 | D. 米 米 |
若对 恒成立,则三角形ABC是( )
恒成立,则三角形ABC是( )
| A.锐角三角形 | B.直角三角形 |
| C.钝角三角形 | D.不能确定形状的三角形 |
给出下列四个命题:
(1)在△ABC中,内角A,B,C的对边分别为a,b,c,且 ,则
,则 ;
;
(2)设 是两个非零向量且
是两个非零向量且 ,则存在实数λ,使得
,则存在实数λ,使得 ;
;
(3)方程 在实数范围内的解有且仅有一个;
在实数范围内的解有且仅有一个;
(4) ;
;
其中正确的个数有
| A.4个 | B.3个 | C.2个 | D.1个 |
在 中,
中, ,面积
,面积 ,则
,则 等于
等于
| A.13 | B. | C. 7 | D. |
已知 中,
中,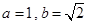 ,
, ,则角
,则角 等于( )
等于( )
A. | B. | C. | D. |
已知锐角 的面积为
的面积为 ,
, ,则角
,则角 的大小为
的大小为
| A.75° | B.60° | C.45° | D.30° |