题目内容
10.数列{an}中,a1=1,a1•a2…an=n2,则a3-a5=( )| A. | $\frac{1}{16}$ | B. | -$\frac{1}{16}$ | C. | $\frac{11}{16}$ | D. | -$\frac{11}{16}$ |
分析 利用数列的递推关系式,逐步求解即可.
解答 解:数列{an}中,a1=1,a1•a2…an=n2,
可得a2=4,
a3=$\frac{{a}_{1}•{a}_{2}•{a}_{3}}{{a}_{1}•{a}_{2}}$=$\frac{9}{4}$,
a5=$\frac{{a}_{1}•{a}_{2}•{a}_{3}•{a}_{4}•{a}_{5}}{{a}_{1}•{a}_{2}•{a}_{3}•{a}_{4}}$=$\frac{25}{16}$.
a3-a5=$\frac{9}{4}-\frac{25}{16}$=$\frac{11}{16}$.
故选:C.
点评 本题考查递推数列的应用,考查计算能力.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
5.函数y=2log4(1-x)的图象大致是( )
| A. | 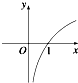 | B. | 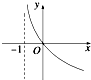 | C. | 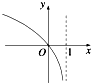 | D. | 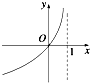 |
2.已知在数列{an}中,a1=1,an=$\frac{{a}_{n-1}}{2{a}_{n-1}+1}$,则a12等于( )
| A. | $\frac{1}{21}$ | B. | $\frac{1}{23}$ | C. | $\frac{1}{25}$ | D. | $\frac{1}{27}$ |
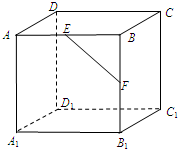 如图,正方体ABCD-A1B1C1D1中E,F分别是棱AB,BB1的中点,则异面直线DD1和EF所成的角的大小为45°.
如图,正方体ABCD-A1B1C1D1中E,F分别是棱AB,BB1的中点,则异面直线DD1和EF所成的角的大小为45°.