题目内容
设f(x)是定义在R上的奇函数,且f(2)=0,当x>0时,有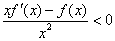 恒成立,则不等式
恒成立,则不等式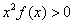 的解集是
的解集是
| A.(-2,0) ∪(2,+∞) | B.(-2,0) ∪(0,2) |
| C.(-∞,-2)∪(2,+∞) | D.(-∞,-2)∪(0,2) |
D
解析试题分析:解:因为当x>0时,有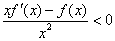 恒成立,即[
恒成立,即[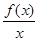 ]′<0恒成立,所以
]′<0恒成立,所以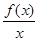 在(0,+∞)内单调递减.因为f(2)=0,所以在(0,2)内恒有f(x)>0;在(2,+∞)内恒有f(x)<0.又因为f(x)是定义在R上的奇函数,所以在(-∞,-2)内恒有f(x)>0;在(-2,0)内恒有f(x)<0.又不等式x2f(x)>0的解集,即不等式f(x)>0的解集.所以答案为(-∞,-2)∪(0,2).故选D.
在(0,+∞)内单调递减.因为f(2)=0,所以在(0,2)内恒有f(x)>0;在(2,+∞)内恒有f(x)<0.又因为f(x)是定义在R上的奇函数,所以在(-∞,-2)内恒有f(x)>0;在(-2,0)内恒有f(x)<0.又不等式x2f(x)>0的解集,即不等式f(x)>0的解集.所以答案为(-∞,-2)∪(0,2).故选D.
考点:函数单调性与导数
点评:本题主要考查函数求导法则及函数单调性与导数的关系,同时考查了奇偶函数的图象特征

练习册系列答案
相关题目
已知函数 的定义域为R,其导函数
的定义域为R,其导函数 的图像如图所示,则对于任意
的图像如图所示,则对于任意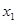 ,
,
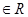 (
(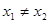 ),下列结论正确的是( )
),下列结论正确的是( )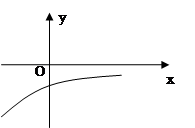
① <0恒成立 ②
<0恒成立 ②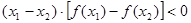 ;③
;③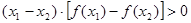 ;
;
④ ;⑤
;⑤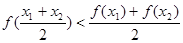 。
。
| A.①③ | B.①③④ | C.②④ | D.②⑤ |
函数f(x)=3+sinx,x∈[0,1)的反函数的定义域是
| A.[0,1) | B.[1,3+sin1) | C.[0,4) | D.[0,+ 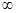 ) ) |
已知函数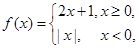 且
且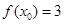 ,则实数
,则实数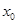 的值为( )
的值为( )
A.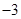 | B.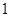 | C.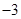 或 或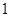 | D.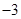 或 或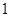 或 或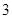 |
f(x)是一次函数且2f(1)+3f(2)=3,2f(-1)-f(0)=-1,则f(x)等于
A.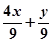 | B.36x-9 | C.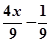 | D.9-36x |
函数f(x)=ln(4+3x-x2)的单调递减区间是
A.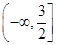 | B.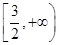 | C.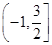 | D.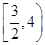 |
函数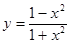 的值域是( )
的值域是( )
| A.[-1,1] | B.(-1,1] | C.[-1,1) | D.(-1,1) |
函数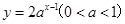 的图象一定过点( )
的图象一定过点( )
| A.(1,1) | B.(1,2) | C.(2,0) | D.(2,-1) |
函数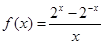 的图象
的图象
| A.关于原点对称 | B.关于y轴对称 | C.关于x轴对称 | D.关于直线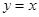 对称 对称 |