题目内容
已知抛物线C:x2=2py(p>0)的焦点为F,定点A(3,2)与点F在C的两侧,C上的动点P到点A的距离与到其准线l的距离之和的最小值为| 10 |
(Ⅰ)求抛物线C的方程;
(Ⅱ)设l与y轴交于点M,过点M任作直线与C交于P,Q两点,Q关于y轴的对称点为Q′.
①求证:Q′,F,P共线;
②求△MPQ′面积S的取值范围.
分析:(Ⅰ)过P作PP1⊥l于P1,则|PA|+|PP1|=|PA|+|PF|≥|AF|.当P,A,F共线时,|PA|+|PP1|取最小值,|AF|=
=
.解得p=6,或p=2,由此能求出抛物线C的方程.
(Ⅱ)①设直线PQ的方程为y=kx-1,由
消去y,整理得x2-4kx+4=0,由△=16k2-16>0,得|k|>1.再由韦达定理知Q′,F,P共线.
②S=
|MF|(|x1|+|-x2|)=
•2•(|x1|+|x2|)=|x1+x2|=4|k|,由|k|>1,知S>4.
9+(
|
| 10 |
(Ⅱ)①设直线PQ的方程为y=kx-1,由
|
②S=
| 1 |
| 2 |
| 1 |
| 2 |
解答: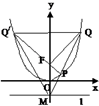 解:(Ⅰ)过P作PP1⊥l于P1,则|PA|+|PP1|=|PA|+|PF|≥|AF|.
解:(Ⅰ)过P作PP1⊥l于P1,则|PA|+|PP1|=|PA|+|PF|≥|AF|.
当P,A,F共线时,|PA|+|PP1|取最小值|AF|=
=
.
解得p=6,或p=2.(3分)
当p=6时,抛物线C的方程为x2=12y,此时,点A与点F在抛物线C同侧,这与已知不符.∴p=2,
抛物线C的方程为x2=4y.(5分)
(Ⅱ)①设直线PQ的方程为y=kx-1,由
消去y,整理得x2-4kx+4=0,
由△=16k2-16>0,得|k|>1.(7分)
设P(x1,y1),Q(x2,y2),则Q′(-x2,y2),x1+x2=4k,x1•x2=4.kFP-kFQ/=
-
=
+
=
=
=0.
∴Q′,F,P共线.(11分)
②S=
|MF|(|x1|+|-x2|)=
•2•(|x1|+|x2|)=|x1+x2|=4|k|,
∵|k|>1,∴S>4.(15分)
 解:(Ⅰ)过P作PP1⊥l于P1,则|PA|+|PP1|=|PA|+|PF|≥|AF|.
解:(Ⅰ)过P作PP1⊥l于P1,则|PA|+|PP1|=|PA|+|PF|≥|AF|.当P,A,F共线时,|PA|+|PP1|取最小值|AF|=
9+(
|
| 10 |
解得p=6,或p=2.(3分)
当p=6时,抛物线C的方程为x2=12y,此时,点A与点F在抛物线C同侧,这与已知不符.∴p=2,
抛物线C的方程为x2=4y.(5分)
(Ⅱ)①设直线PQ的方程为y=kx-1,由
|
由△=16k2-16>0,得|k|>1.(7分)
设P(x1,y1),Q(x2,y2),则Q′(-x2,y2),x1+x2=4k,x1•x2=4.kFP-kFQ/=
| y1-1 |
| x1 |
| y2-1 |
| -x2 |
| kx1-2 |
| x1 |
| kx2-2 |
| x2 |
| 2kx1x2-2(x1+x2) |
| x1x2 |
| 2k•4-2•4k |
| 4 |
∴Q′,F,P共线.(11分)
②S=
| 1 |
| 2 |
| 1 |
| 2 |
∵|k|>1,∴S>4.(15分)
点评:本题考查直线和圆锥曲线的位置关系,计算量较大,计算过程较繁,解题时要认真审题,合理地进行等价变换,注意提高解题技巧.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目