题目内容
13.已知向量$\overrightarrow{a}•\overrightarrow{b}$=0且($\overrightarrow{a}-\overrightarrow{c}$)•($\overrightarrow{b}-\overrightarrow{c}$)=0,|$\overrightarrow{a}-\overrightarrow{c}$|=$\sqrt{3}$,|$\overrightarrow{b}-\overrightarrow{c}$|=1,则|$\overrightarrow{a}+\overrightarrow{c}$|的最大值为3,$\overrightarrow{a}•\overrightarrow{c}$的最大值为$\frac{3}{2}$.分析 由$\overrightarrow{a}•\overrightarrow{b}$=0,建立直角坐标系.可设$\overrightarrow{a}$=(m,0),$\overrightarrow{b}$=(0,n),$\overrightarrow{c}$=(x,y),由($\overrightarrow{a}-\overrightarrow{c}$)•($\overrightarrow{b}-\overrightarrow{c}$)=0,可得点C满足$(x-\frac{m}{2})^{2}+(y-\frac{n}{2})^{2}=\frac{{m}^{2}+{n}^{2}}{4}$.画出图形,设∠CBD=θ,把$\overrightarrow{a}、\overrightarrow{c}$的坐标用含有θ的代数式表示,然后结合三角函数求最值得答案.
解答 解:由$\overrightarrow{a}•\overrightarrow{b}$=0,建立如图所示的直角坐标系.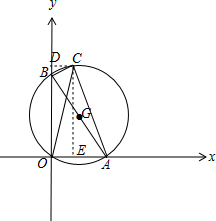
可设$\overrightarrow{a}$=$\overrightarrow{OA}$=(m,0),$\overrightarrow{b}$=$\overrightarrow{OB}$=(0,n),$\overrightarrow{c}$=$\overrightarrow{OC}$=(x,y),
由($\overrightarrow{a}-\overrightarrow{c}$)•($\overrightarrow{b}-\overrightarrow{c}$)=0,得(m-x,-y)•(-x,n-y)=0
即x2-mx+y2-ny=0,化为$(x-\frac{m}{2})^{2}+(y-\frac{n}{2})^{2}=\frac{{m}^{2}+{n}^{2}}{4}$.
∵|$\overrightarrow{a}-\overrightarrow{c}$|=$\sqrt{3}$,|$\overrightarrow{b}-\overrightarrow{c}$|=1,
∴|AC|=$\sqrt{3}$,|BC|=1,
设∠CBD=θ,则∠OAC=θ.
则x=sinθ=m-$\sqrt{3}$cosθ,
∵|$\overrightarrow{a}+\overrightarrow{c}$|=|(2sinθ+$\sqrt{3}cosθ$,$\sqrt{3}sinθ$)|=$\sqrt{4sin(2θ-\frac{π}{6})+5}$.
∴|$\overrightarrow{a}+\overrightarrow{c}$|的最大值为3;
∵$\overrightarrow{a}•\overrightarrow{c}$=mx=sinθ(sinθ+$\sqrt{3}$cosθ)
=sin2θ+$\sqrt{3}$sinθcosθ
=$\frac{1}{2}$(1-cos2θ)+$\frac{\sqrt{3}}{2}$sin2θ
=sin(2θ-$\frac{π}{6}$)+$\frac{1}{2}$≤$\frac{3}{2}$.
∴$\overrightarrow{a}•\overrightarrow{c}$的最大值为$\frac{3}{2}$.
故答案为:3;$\frac{3}{2}$.
点评 本题综合考查了向量的坐标运算、向量垂直与数量积的关系、数量积的性质、三角函数代换等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

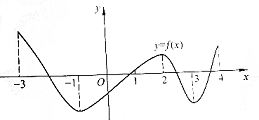 已知函数y=f(x)在区间[-3,4]上的图象如图所示,根据图象说出函数的单调区间,以及在每一个区间上函数的单调性.
已知函数y=f(x)在区间[-3,4]上的图象如图所示,根据图象说出函数的单调区间,以及在每一个区间上函数的单调性.