题目内容
已知定义域在R上的函数f(x)，对任意的x，y∈R均有：f(x＋y)＋f(x－y)＝2f(x)·f(y)，且f(0)≠0．
(1)求f(0)的值；
(2)判断f(x)的奇偶性．
答案：
解析：
解析：
|
解：(1)令 因为 所以 (2)令 所以 即有： 所以 |
，则有
，
，
． 4分
，则有
，由
，
，
是偶函数． 12分
练习册系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
=（x，1），
=（-1，b-x），函数f（x）=a-
是偶函数．
已知下表为定义域为R的函数f（x）=ax3+cx+d若干自变量取值及其对应函数值，为便于研究，相关函数值非整数值时，取值精确到0.01．
根据表中数据解答下列问题：
（1）函数y=f（x）在区间[0.55，0.6]上是否存在零点，写出判断并说明理由；
（2）证明：函数y=f（x）在区间（-∞，-0.35]单调递减．
| x | 3.27 | 1.57 | -0.61 | -0.59 | 0.26 | 0.42 | -0.35 | -0.56 | 4.25 | |
| y | -101.63 | -10.04 | 0.07 | 0.03 | 0.21 | 0.20 | -0.22 | -0.03 | -226.05 |
（1）函数y=f（x）在区间[0.55，0.6]上是否存在零点，写出判断并说明理由；
（2）证明：函数y=f（x）在区间（-∞，-0.35]单调递减．
=（x，1），
=（-1，b-x），函数f（x）=a-
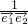是偶函数．