题目内容
已知正方体的棱长为2,则它的内切球的表面积是
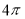
【解析】
试题分析:此正方体内切球的直径为2,即半径为1.所以此正方体内切球的表面积为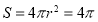 。
。
考点:正方体的内切球及球的表面积公式。

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
题目内容
已知正方体的棱长为2,则它的内切球的表面积是
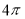
【解析】
试题分析:此正方体内切球的直径为2,即半径为1.所以此正方体内切球的表面积为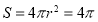 。
。
考点:正方体的内切球及球的表面积公式。

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案