题目内容
对正整数n,设曲线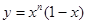 在x=2处的切线与y轴交点的纵坐标为
在x=2处的切线与y轴交点的纵坐标为 ,则数列
,则数列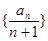 的前n项和等于 .
的前n项和等于 .

解析考点:数列的求和;导数的几何意义.
分析:先求出x=2时曲线方程的导函数,进而可知切线方程,令x=0进而求得数列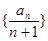 的通项公式,可得数列{an}的通项公式,最后用错位相减法求得答案.
的通项公式,可得数列{an}的通项公式,最后用错位相减法求得答案.
解:∵y’|x=2=-2n-1(n+2),
∴切线方程为:y+2n=-2n-1(n+2)(x-2),
令x=0,求出切线与y轴交点的纵坐标为y0=(n+1)2n,
所以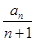 =2n,则数列{
=2n,则数列{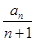 }的前n项和Sn=
}的前n项和Sn=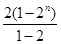 =2n+1-2
=2n+1-2

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在x=2处的切线与y轴交点的纵坐标为
在x=2处的切线与y轴交点的纵坐标为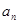 ,则
,则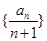 的前n项和是
.
的前n项和是
.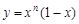 在x=2处的切线与y轴交点的纵坐标为
在x=2处的切线与y轴交点的纵坐标为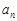 ,则数列
,则数列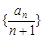 的前n项和的公式是
的前n项和的公式是