题目内容
已知下列命题:①“若x2+y2=0,则实数x、y全为零”的逆否命题;②“矩形是平行四边形”的逆命题;③“若m>2,则x2-2x+m>0的解集为R”的逆否命题;④“若a>b,则ac2>bc2”的逆命题.⑤把函数y=sin(-2x)(x∈R)的图象上所有的点向右平移 个单位即可得到函数
个单位即可得到函数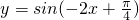 (x∈R)的图象其中真命题是________(只写序号)
(x∈R)的图象其中真命题是________(只写序号)
①③④⑤
分析:由于原命题与其逆否命题为等价命题,故①与③的逆否命题的真假判断,只需判断与①与③的真假即可;
②“矩形是平行四边形”的逆命题为:“平行四边形是矩形”,显然错;
④“若a>b,则ac2>bc2”的逆命题“若ac2>bc2,则a>b”正确;
利用三角函数的平移法则可判断⑤的正误.
解答:∵“若x2+y2=0,则实数x、y全为零”为真命题,其原命题与其逆否命题为等价命题,
∴其逆否命题为真命题,故①正确;
对于③:由于m>2,x2-2x+m>0中,△=4-4m<0,故x2-2x+m>0的解集为R,
∴“若m>2,则x2-2x+m>0的解集为R”为真命题,从而其逆否命题亦为真命题;
②“矩形是平行四边形”的逆命题为:“平行四边形是矩形”,显然错;
④“若a>b,则ac2>bc2”的逆命题“若ac2>bc2,则a>b”,正确;
对于⑤函数y=sin(-2x)(x∈R) y=sin[-2(x-
y=sin[-2(x- )=sin(-2x+
)=sin(-2x+ ),
),
故⑤正确.
综上所述正确答案为:①③④⑤.
故答案为:①③④⑤
点评:本题考查命题的真假判断与应用,着重考查四种命题间的关系,特别是“原命题与其逆否命题为等价命题”的利用,
属于中档题.
分析:由于原命题与其逆否命题为等价命题,故①与③的逆否命题的真假判断,只需判断与①与③的真假即可;
②“矩形是平行四边形”的逆命题为:“平行四边形是矩形”,显然错;
④“若a>b,则ac2>bc2”的逆命题“若ac2>bc2,则a>b”正确;
利用三角函数的平移法则可判断⑤的正误.
解答:∵“若x2+y2=0,则实数x、y全为零”为真命题,其原命题与其逆否命题为等价命题,
∴其逆否命题为真命题,故①正确;
对于③:由于m>2,x2-2x+m>0中,△=4-4m<0,故x2-2x+m>0的解集为R,
∴“若m>2,则x2-2x+m>0的解集为R”为真命题,从而其逆否命题亦为真命题;
②“矩形是平行四边形”的逆命题为:“平行四边形是矩形”,显然错;
④“若a>b,则ac2>bc2”的逆命题“若ac2>bc2,则a>b”,正确;
对于⑤函数y=sin(-2x)(x∈R)
 y=sin[-2(x-
y=sin[-2(x- )=sin(-2x+
)=sin(-2x+ ),
),故⑤正确.
综上所述正确答案为:①③④⑤.
故答案为:①③④⑤
点评:本题考查命题的真假判断与应用,着重考查四种命题间的关系,特别是“原命题与其逆否命题为等价命题”的利用,
属于中档题.

练习册系列答案
相关题目