题目内容
已知函数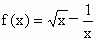 ,求证:
,求证:
(1)f(x)在定义域上是增函数;
(2)满足等式f(x)=1的实数x的值至多只有一个.
答案:略
解析:
提示:
解析:
|
证明: (1)函数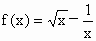 的定义域是(0,+¥
). 的定义域是(0,+¥
).
设 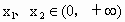 ,且 ,且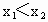 ,则 ,则
∵
∴ (2)设 若 若 ∴ |
提示:
|
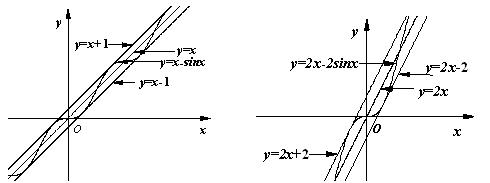
问题 (2)通过图像更易于理解,由 ,得 ,得 .在同一坐标系中作出函数 .在同一坐标系中作出函数 与 与 的图像,如图所示,可以看出,满足等式f(x)=1的实数x的值有且只有一个. 的图像,如图所示,可以看出,满足等式f(x)=1的实数x的值有且只有一个.
|

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
,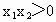 ,
,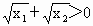 .
.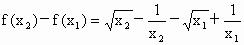
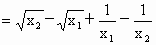
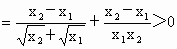 .
.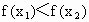 ,即f(x)在定义域上为增函数.
,即f(x)在定义域上为增函数.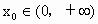 满足等式f(x)=1,即
满足等式f(x)=1,即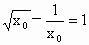 ,假设满足等式f(x)=1的实数x的值至少有两个,不妨设
,假设满足等式f(x)=1的实数x的值至少有两个,不妨设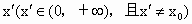 也满足f(x)=1,即
也满足f(x)=1,即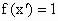 ,
,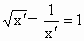 .
.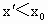 ,由(1)知
,由(1)知 ,
,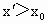 ,由(1)知
,由(1)知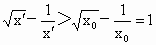 .
.


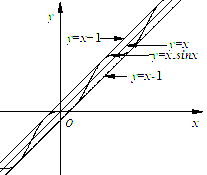

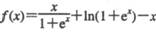 .
.
 时,
时,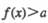 恒成立?若存在,求a的取值范围,若不存在,说明理由.
恒成立?若存在,求a的取值范围,若不存在,说明理由.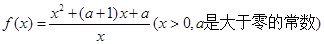 .
.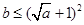 是
是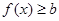 的充要条件;
的充要条件;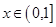 时,
时, 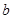 的取值范围.
的取值范围.