Question

设直线. 若直线l与曲线S同时满足下列两个条件：①直线l与曲线S相切且至少有两个切点；②对任意x∈R都有. 则称直线l为曲线S的“上夹线”．

（Ⅰ）已知函数．求证：为曲线的“上夹线”．

（Ⅱ）观察下图：

          

   

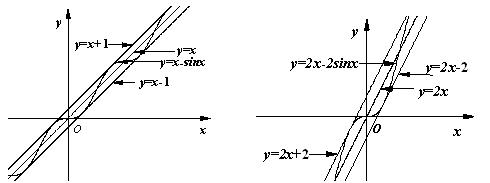
根据上图，试推测曲线的“上夹线”的方程，并给出证明．

Answer 1

（Ⅰ）证明见解析（Ⅱ）推测：的“上夹线”的方程为 

解析:

（Ⅰ）由得，                

当时，，此时，， 

，所以是直线与曲线的一个切点；    

当时，，此时，，          

，所以是直线与曲线的一个切点；     

所以直线l与曲线S相切且至少有两个切点；

对任意x∈R，，

所以       

因此直线是曲线的“上夹线”．      

（Ⅱ）推测：的“上夹线”的方程为      

①先检验直线与曲线相切，且至少有两个切点：

设：

 ，令，得：（kZ）            

当时,

故：过曲线上的点(，)的切线方程为：

y－[]= [－()]，化简得：．

即直线与曲线相切且有无数个切点．    -

不妨设

②下面检验g(x)F(x)

g(x)－F(x)=

直线是曲线的“上夹线”．