题目内容
（2012•海淀区一模）过双曲线
-
=1的右焦点，且平行于经过一、三象限的渐近线的直线方程是（ ）
| x2 |
| 9 |
| y2 |
| 16 |
分析：由双曲线
-
=1的右焦点为F（5，0），经过一、三象限的渐近线为y=
x，得到所求直线方程为y=
(x-5)，由此能够求出结果．
| x2 |
| 9 |
| y2 |
| 16 |
| 4 |
| 3 |
| 4 |
| 3 |
解答：解：∵双曲线
-
=1的右焦点为F（5，0），
经过一、三象限的渐近线为y=
x，
∴所求直线方程为y=
(x-5)，
整理，得4x-3y-20=0．
故选D．
| x2 |
| 9 |
| y2 |
| 16 |
经过一、三象限的渐近线为y=
| 4 |
| 3 |
∴所求直线方程为y=
| 4 |
| 3 |
整理，得4x-3y-20=0．
故选D．
点评：本题考查双曲线的简单性质的应用，是基础题．解题时要认真审题，仔细解答．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
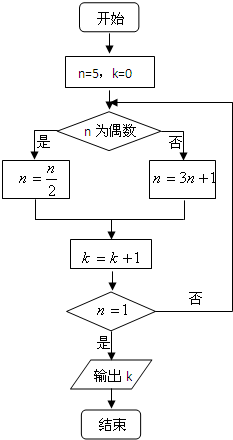（2012•海淀区一模）执行如图所示的程序框图，输出的k值是（ ）
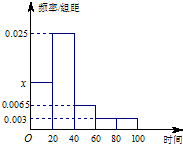（2012•海淀区一模）某学校随机抽取部分新生调查其上学所需时间（单位：分钟），并将所得数据绘制成频率分布直方图（如图），其中，上学所需时间的范围是[0，100]，样本数据分组为[0，20），[20，40），[40，60），[60，80），[80，100]．