题目内容
（2012•海淀区一模）从甲、乙等5个人中选出3人排成一列，则甲不在排头的排法种数是（ ）
分析：先分类：（1）不选甲，有
种选法；（2）选甲，共
•
种，相加可得．
| A | 3 4 |
| C | 1 2 |
| A | 2 4 |
解答：解：（1）若不选甲，则有
=24种选法；
（2）若选甲，则先从令两个位置中选一个给甲，
再从其余的4人中选2人排列，共有
•
=24种，
由分类计数原理可得总的方法种数为24+24=48，
故选D
| A | 3 4 |
（2）若选甲，则先从令两个位置中选一个给甲，
再从其余的4人中选2人排列，共有
| C | 1 2 |
| A | 2 4 |
由分类计数原理可得总的方法种数为24+24=48，
故选D
点评：本题考查简单的排列组合问题，涉及分类计数，和分步计数原理，属中档题．
练习册系列答案
金钥匙试卷系列答案
相关题目
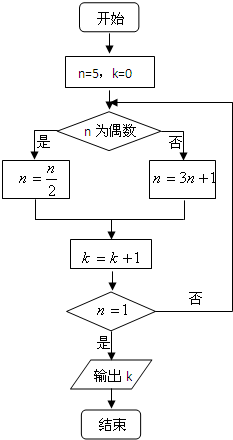（2012•海淀区一模）执行如图所示的程序框图，输出的k值是（ ）
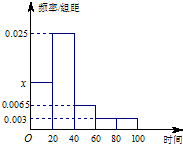（2012•海淀区一模）某学校随机抽取部分新生调查其上学所需时间（单位：分钟），并将所得数据绘制成频率分布直方图（如图），其中，上学所需时间的范围是[0，100]，样本数据分组为[0，20），[20，40），[40，60），[60，80），[80，100]．