题目内容
6.解不等式:$\frac{{x}^{2}-3x-10}{{x}^{2}-7x+6}$>0.分析 把不等式$\frac{{x}^{2}-3x-10}{{x}^{2}-7x+6}$>0化为等价的不等式组$\left\{\begin{array}{l}{{x}^{2}-3x-10>0}\\{{x}^{2}-7x+6>0}\end{array}\right.$或$\left\{\begin{array}{l}{{x}^{2}-3x-10<0}\\{{x}^{2}-7x+6<0}\end{array}\right.$,求出它们的解集即可.
解答 解:不等式$\frac{{x}^{2}-3x-10}{{x}^{2}-7x+6}$>0可化为不等式组
$\left\{\begin{array}{l}{{x}^{2}-3x-10>0}\\{{x}^{2}-7x+6>0}\end{array}\right.$①,
或$\left\{\begin{array}{l}{{x}^{2}-3x-10<0}\\{{x}^{2}-7x+6<0}\end{array}\right.$②;
解①得,x<-2或x>6;
解②得,1<x<5;
综上,原不等式的解集为{x|x<-2或1<x<5或x>6}.
点评 本题考查了分式不等式的解法与应用问题,解题的关键是把分式不等式化为等价的不等式组,是基础题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.已知f(x)=2x+1,g(x)=2x-1,则不等式f[g(x)]>g[f(x)]的解集是( )
| A. | {x|x<2} | B. | {x|0<x<2} | C. | {x|x>2} | D. | {x|1<x<2} |
11.若定义在[1,16]上的函数f(x)=$\left\{\begin{array}{l}4-8\left|{x-\left.{\frac{3}{2}}\right|}\right.\;,\;1≤x≤2\\ \frac{1}{2}f(\frac{x}{2})\;\;\;\;\;,\;2<x≤16\end{array}$,则下列结论中错误的是( )
| A. | 函数f(x)的值域为[0,4] | B. | 函数f(x)在[8,12]单调递增 | ||
| C. | 关于x的方程2f(x)-1=0有6个根 | D. | 不等式xf(x)≤6恒成立 |
18.已知函数f(x)=x3-3ax+1有3个零点,则a的取值范围为( )
| A. | (0,$\frac{\sqrt{2}}{2}$) | B. | ($\frac{\sqrt{2}}{2}$,+∞) | C. | (0,$\frac{\sqrt{2}}{2}$) | D. | ($\frac{\root{3}{2}}{2}$,+∞) |
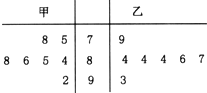 青年歌手大奖赛共有10名选手参赛,并请了7名评委,如茎叶图是7名评委给参加最后决赛的两位选手甲、乙评定的成绩,去掉一个最高分和一个最低分后,甲、乙选手剩余数据的平均成绩分别为84.2,85.
青年歌手大奖赛共有10名选手参赛,并请了7名评委,如茎叶图是7名评委给参加最后决赛的两位选手甲、乙评定的成绩,去掉一个最高分和一个最低分后,甲、乙选手剩余数据的平均成绩分别为84.2,85.