题目内容
已知函数f(x) =2x+1,x∈R.规定:给定一个实数x0,赋值x1= f(x0),若x1≤255,则继续赋值x2=" f(x1)" …,以此类推,若x n-1≤255,则xn= f(xn-1),否则停止赋值,如果得到xn后停止,则称赋值了n次(n∈N *).已知赋值k次后该过程停止,则x0的取值范围是
| A.(2k-9 ,2 k-8] | B.(2 k-8 -1, 2k-9-1] | C.(28-k -1, 29-k-1] | D.(27-k -1, 28-k-1] |
C
提示1:由题意,可先解出x1,x2,x3,从中发现规律,猜想出xk=f(xk-1)=2xk-1-1=2kx0-2k-1-…-22-2-1=2kx0
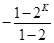 =2kx0-2k+1,再由题设条件xn-1≤257,则xn=f(xn-1),否则停止赋值,可得到2kx0-2k+1>257,且2k-1x0-2k-1+1≤257,解此二不等式即可得到x0的取值范围选出正确选项.
=2kx0-2k+1,再由题设条件xn-1≤257,则xn=f(xn-1),否则停止赋值,可得到2kx0-2k+1>257,且2k-1x0-2k-1+1≤257,解此二不等式即可得到x0的取值范围选出正确选项.提示2:本题考查归纳推理,等比数列的求和公式,解题的特点是先列举几个特殊例子找出规律,从而利用规律得出结论,解答本题,理解赋值终止的条件是关键
解:由题意x1=f(x0)=2x0-1;
x2=f(x1)=2x1-1=2(2x0-1)-1=22x0-2-1;
x3=f(x2)=2x2-1=2(22x0-2-1)-1=23x0-22-2-1;
…,
xk=f(xk-1)=2xk-1-1=2kx0-2k-1-…-22-2-1=2kx0-
 =2kx0-2k+1;
=2kx0-2k+1;令2kx0-2k+1>257,且2k-1x0-2k-1+1≤257,
解得28-k+1<x0≤29-k+1
故x0的取值范围是(28-k+1,29-k+1]
故选C

练习册系列答案
相关题目
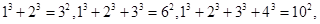 根据上述规律写出第六个等式为 .
根据上述规律写出第六个等式为 . ,
,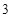 ,
,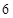 ,
,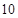 ,
,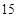 ,
,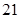 ,
,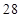 ,… 这些数叫做三角形数.则
,… 这些数叫做三角形数.则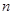 个三角形数为 ( )
个三角形数为 ( )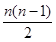
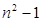
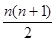
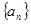 中,若
中,若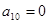 ,则有等式
,则有等式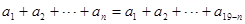
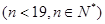 成立,类比上述性质,在等比数列
成立,类比上述性质,在等比数列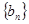 中,若
中,若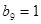 ,则有等式 .
,则有等式 .
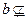 平面
平面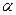 ,直线
,直线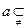 平面
平面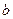 ∥平面
∥平面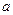 ”的结论显然是错误的,这是因为
”的结论显然是错误的,这是因为 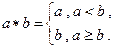 已知
已知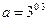 ,
, ,
, ,则
,则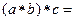 .
. ,
,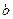 ,
,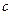 表示)
表示) ,若
,若 ,求实数
,求实数 的值。
的值。 他
他