题目内容
一圆与y轴相切,圆心在直线x-3y=0上,且直线y=x截圆所得弦长为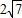 ,求此圆的方程.
,求此圆的方程.
【答案】分析:依题意设出所求圆的方程:(x-3b)2+(y-b)2=9b2.利用直线y=x截圆所得弦长为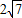 ,
,
求出b的值,可得圆的方程.
解答:解:因圆与y轴相切,且圆心在直线x-3y=0上,故设圆方程为(x-3b)2+(y-b)2=9b2.
又因为直线y=x截圆得弦长为2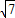 ,
,
则有(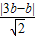 )2+(
)2+(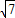 )2=9b2,
)2=9b2,
解得b=±1.故所求圆方程为
(x-3)2+(y-1)2=9或(x+3)2+(y+1)2=9.
点评:本题考查圆的标准方程,圆心到直线的距离,是基础题.
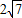 ,
,求出b的值,可得圆的方程.
解答:解:因圆与y轴相切,且圆心在直线x-3y=0上,故设圆方程为(x-3b)2+(y-b)2=9b2.
又因为直线y=x截圆得弦长为2
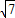 ,
,则有(
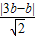 )2+(
)2+(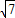 )2=9b2,
)2=9b2,解得b=±1.故所求圆方程为
(x-3)2+(y-1)2=9或(x+3)2+(y+1)2=9.
点评:本题考查圆的标准方程,圆心到直线的距离,是基础题.

练习册系列答案
相关题目
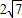 ,求此圆的方程.
,求此圆的方程.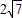 ,求此圆的方程.
,求此圆的方程.