题目内容
一圆与y轴相切,圆心在直线x-3y=0上,在y=x上截得的弦长为2| 7 |
(1)求此圆的方程.
(2)设M(x,y)是此圆上一点,O为坐标原点,求直线OM的斜率的取值范围.
分析:(1)由圆心坐标为(a,b),半径为r,设出圆的标准方程,根据圆与y轴相切,得到圆的半径等于圆心横坐标的绝对值,把圆心坐标代入直线x-3y=0,得到关于a与b的方程,再由垂径定理得到弦心距,弦的一半及圆的半径构成的直角三角形,利用勾股定理表示出一个关系式,三者联立即可求出a,b及r的值,从而确定出圆的方程;
(2)根据直线OM过原点,设斜率为k,写出直线OM的方程,代入第一问求出的圆的方程,消去y后得到关于x的一元二次方程,令根的判别式大于等于0列出关于k的不等式,求出不等式的解集即可得到k的范围.
(2)根据直线OM过原点,设斜率为k,写出直线OM的方程,代入第一问求出的圆的方程,消去y后得到关于x的一元二次方程,令根的判别式大于等于0列出关于k的不等式,求出不等式的解集即可得到k的范围.
解答:解:(1)设所求圆的方程为(x-a)2+(y-b)2=r2(r>0),
则
,解得
或
.(4分)
所以,所求圆的方程为(x-3)2+(y-1)2=9或(x+3)2+(y+1)2=9.(6分)
(2)设直线OM方程为y=kx,代入所求出的圆的方程,
整理得(1+k2)x2-(6+2k)x+1=0或(1+k2)x2+(6+2k)x+1=0,
由判别式△≥0,解得k≥-
.(10分)
则
|
|
|
所以,所求圆的方程为(x-3)2+(y-1)2=9或(x+3)2+(y+1)2=9.(6分)
(2)设直线OM方程为y=kx,代入所求出的圆的方程,
整理得(1+k2)x2-(6+2k)x+1=0或(1+k2)x2+(6+2k)x+1=0,
由判别式△≥0,解得k≥-
| 4 |
| 3 |
点评:此题考查了直线与圆相交的性质,要求学生掌握垂径定理,勾股定理及方程有解时根的判别式大于等于0这个结论,会利用待定系数法求圆的方程.

练习册系列答案
相关题目
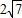 ,求此圆的方程.
,求此圆的方程.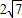 ,求此圆的方程.
,求此圆的方程.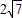 ,求此圆的方程.
,求此圆的方程.