题目内容

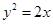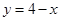(本小题满分12分)求抛物线与直线围成的平面图形的面积

 

【答案】

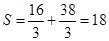
【解析】本试题主要是考查了定积分的几何意义的运用，表示曲边梯形的面积的运算。先求解交点，确定上限和下限，然后利用定积分的基本定理得到结论。

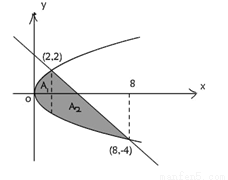
解：由方程组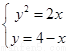解得抛物线与直线的交点为（2，2），（8，-4）取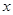为积分变量，由下图可得

 ；　

　

 

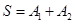
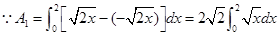
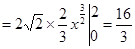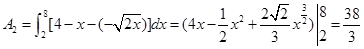
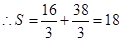
练习册系列答案
相关题目
（文） （本小题满分12分已知函数y=4-2
3
sinx•cosx-2sin2x(x∈R)，
（1）求函数的值域和最小正周期；
（2）求函数的递减区间．
（2011•自贡三模）（本小题满分12分＞
设平面直角坐标中，O为原点，N为动点，|
ON
|=6，
ON
=
5
•
OM
．过点M作MM1丄y轴于M1，过N作NN1⊥x轴于点N1，
OT
=
M1M
+
N1N
，记点T的轨迹为曲线C．
（I）求曲线C的方程：
（H）已知直线L与双曲线C：5x2-y2=36的右支相交于P、Q两点（其中点P在第-象限）．线段OP交轨迹C于A，若
OP
=3
OA
，S△PAQ=-26tan∠PAQ求直线L的方程．

（本小题满分12分）已知函数，且。①求的最大值及最小值；②求的在定义域上的单调区间.

（2009湖南卷文）（本小题满分12分）

为拉动经济增长，某市决定新建一批重点工程，分别为基础设施工程、民生工程和产业建设工程三类，这三类工程所含项目的个数分别占总数的、、.现有3名工人独立地从中任选一个项目参与建设.求：

（I）他们选择的项目所属类别互不相同的概率；    w.w.w.k.s.5.u.c.o.m    

（II）至少有1人选择的项目属于民生工程的概率.

（本小题满分12分）

某民营企业生产A，B两种产品，根据市场调查和预测，A产品的利润与投资成正比，其关系如图1，B产品的利润与投资的算术平方根成正比，其关系如图2，

（注：利润与投资单位是万元）

（1）分别将A，B两种产品的利润表示为投资的函数，并写出它们的函数关系式.（2）该企业已筹集到10万元资金，并全部投入到A，B两种产品的生产，问：怎样分配这10万元投资，才能使企业获得最大利润，其最大利润为多少万元.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网