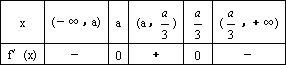题目内容
设函数f(x)＝－x(x－a)2(x∈R)，其中a∈R．
(Ⅰ)当a＝1时，求曲线y＝f(x)在点(2，f(2))处的切线方程；
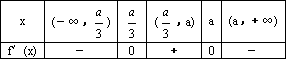
(Ⅱ)当a≠0时，求函数f(x)的极大值和极小值；
(Ⅲ)当a＞3时，在区间[－1，0]上是否存在实数k使不等式f(k－cosx)≥f(k2－cos2x)对任意的x∈R恒成立，若存在，求出k的值，若不存在，说明理由．
答案：
解析：
解析：
|
解：(Ⅰ)当 所以，曲线 整理得 (Ⅱ)解： 令 由于 (1)若
因此，函数 函数 (2)若
因此，函数 函数 (Ⅲ)假设在区间 由 由(Ⅱ)知， 要使 只要 即 设 要使①式恒成立，必须 所以，在区间 |
时，
，得
，且
，
．
在点
处的切线方程是
，
；4分
．
，解得
或
；5分
，以下分两种情况讨论．
，当
变化时，
的正负如下表：
在
处取得极小值
，且
；
在
处取得极大值
，且
；7分
，当
变化时，
的正负如下表：
在
处取得极小值
，且
；
在
处取得极大值
，且
．9分
上存在实数
满足题意．
，得
，当
时，
，
；10分
在
上是减函数，
，
①；12分
，则函数
在
上的最大值为
．
，即
或
．
，使得
对任意的
练习册系列答案
相关题目
)－1(ω＞0)的导数
(x)最大值为3，则f(x)的图像的一条对称轴的方程是
(x＞0)，观察：f1(x)＝f(x)＝
，f2(x)＝f(f1(x))＝
，f3(x)＝f(f2(x))＝
，f4(x)＝f(f3(x))＝
，……根据以上事实，由归纳推理可得：当n∈N+且n≥2时，fn(x)＝f(fn－1(x))＝________．
，且f(1)＝7，设F(x)＝f(x)－ax2(a∈R)．
．
(a，b为常数)，且方程f(x)＝
有两个实根为x1＝－1，x2＝2．