题目内容
已知递减的等差数列{an}满足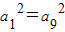
，则a5=（ ）A．-1
B．0
C．-1或0
D．4或5
【答案】分析：由题意可得（a9+a1）（a9-a1）=0，a9=-a1，由此利用等差数列的性质可得a5 =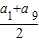
的值．
解答：解：已知递减的等差数列{an}满足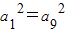
，则 （a9+a1）（a9-a1）=0，
故有 a9=-a1，∴a5 =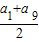
=0，
故选 B．
点评：本题主要考查等差数列的定义和性质，求得a9=-a1，是解题的关键，属于中档题．
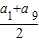的值．解答：解：已知递减的等差数列{an}满足
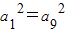，则 （a9+a1）（a9-a1）=0，故有 a9=-a1，∴a5 =
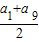=0，故选 B．
点评：本题主要考查等差数列的定义和性质，求得a9=-a1，是解题的关键，属于中档题．
练习册系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
已知递减的等差数列{an}满足a12=a92，则数列{an}的前n项和Sn取最大值时，n=（ ）
| A、3 | B、4 | C、4或5 | D、5或6 |
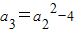，则an= ．