题目内容
已知递减的等差数列{an}满足a1=1,a3=a22-4,则an=______.
设等差数列{an}的公差为d,由a3=a22-4得,
a1+2d=(a1+d)2-4,即1+2d=(1+d)2-4,
解得d2=4,d=±2,
∵等差数列{an}是递减数列,∴d=-2,
∴an=1+-2(n-1)=-2n+3,
故答案为:-2n+3.
a1+2d=(a1+d)2-4,即1+2d=(1+d)2-4,
解得d2=4,d=±2,
∵等差数列{an}是递减数列,∴d=-2,
∴an=1+-2(n-1)=-2n+3,
故答案为:-2n+3.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
已知递减的等差数列{an}满足a12=a92,则数列{an}的前n项和Sn取最大值时,n=( )
| A、3 | B、4 | C、4或5 | D、5或6 |
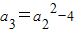 ,则an= .
,则an= .