Question

函数f（x）=x²+bln（x+1）-2x，b∈R．
（1）当b=1时，求曲线f（x）在点（0，f（0））处的切线方程；([ln(x+1)]′=

1

x+1

)
（2）当b=

3

2

时，求函数f（x）在（-1，1]上的最大值；（ln2≈0.69）
（3）设g（x）=f（x）+2x，若b≥2，求证：对任意x₁，x₂∈（-1，+∞），且x₁≥x₂，都有g（x₁）-g（x₂）≥2（x₁-x₂）．

Answer 1

分析：（1）把b=1代入解析式，使得解析式具体，对于函数求导利用导函数的几何意义即可求的；
（2）把b=

3

2

代入解析式，由函数求导得导函数，求出函数在定义域上的极值，在与区间端点值进行比较大小，进而求得函数在区间上的最值；
（3）由于g（x）=f（x）+2x，由函数解析式求导得其导函数，利用导函数得到函数在区间上的单调性，进而得到要证明的不等式．

解答：解：（1）当b=1时，f（x）=x²+ln（x+1）-2x定义域为（-1，+∞），
f′(x)=2x+

1

x+1

-2，f^′（0）=-1，又f（0）=0，
故有直线的方程可知：曲线f（x）在点（0，f（0））出的切线方程为：y=-x，
（2）当b=

3

2

时，f(x)=x2+

3

2

ln(x+1)-2x，
求导得：f′(x)=2x+

3

2(x+1)

 -2=

4x2-1

2(x+1)

，
由f^′（x）=0⇒x=±

1

2

，
当x变化时，f^′（x），f（x）的变化情况如下表：

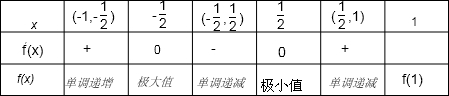
由上表可知：f(x)极大值=f(-

1

2

)=

5

4

-

3

2

ln2，f(1)=

3

2

ln2-1，而f(-

1

2

)-f(1)=

9

4

-3ln2＞2.25-2.1=0.15＞0，
所以f(-

1

2

)＞f(1)，所以函数f（x）在（-1，1]上的最大值为：

5

4

-

3

2

ln2，
（3）证明：∵f（x）=x²+bln（x+1）-2x
∴f′(x)=2x+

b

x+1

-2=2(x+1)+

b

x+1

-4   ≥2

2(x+1)• b x+1

-4=2

2b

-4≥2

2×2

-4=0．
当且仅当2（x+1）=

b

x+1

，即：b=2，且x=0时取等号，
∴b≥2时，函数f（x）在（-1，+∞）内单调递增，从而对于任意x₁，x₂∈（-1，+∞）且x₁≥x₂，有f（x₁）＞f（x₂），即
g（x₁）-2x₁≥g（x₂）-2x₂∴g（x₁）-g（x₂）≥2（x₁-x₂）

点评：此题考查了利用导数求函数在闭区间上的最值，还考查了导数的几何含义进而求出曲线上任意一点处的切线方程，还考查了利用均值不等式求解函数的最值．