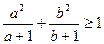题目内容
(本小题满分10分)已知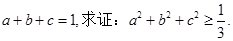
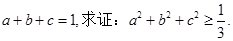
见解析。
本试题主要是考查了不等式的证明。利用重要不等式来证明成立。先a+b+c="1" 左右两边分别平方得
a²+b²+c²+2ab+2bc+2ac=1
然后可知a²+b²+c²≥1/3证明之。
证明:a+b+c="1" 左右两边分别平方得
a²+b²+c²+2ab+2bc+2ac=1
得2ab+2bc+2ac=1-(a²+b²+c²)≤a²+b²+b²+c²+a²+c²
整理得3(a²+b²+c²)≥1
所以 a²+b²+c²≥1/3
当且仅当a="b=c=1/3" a²+b²+c²=1/3
a²+b²+c²+2ab+2bc+2ac=1
然后可知a²+b²+c²≥1/3证明之。
证明:a+b+c="1" 左右两边分别平方得
a²+b²+c²+2ab+2bc+2ac=1
得2ab+2bc+2ac=1-(a²+b²+c²)≤a²+b²+b²+c²+a²+c²
整理得3(a²+b²+c²)≥1
所以 a²+b²+c²≥1/3
当且仅当a="b=c=1/3" a²+b²+c²=1/3

练习册系列答案
相关题目
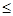
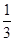 ;
;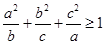
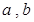 为实数,证明:
为实数,证明: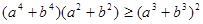 .
.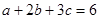 ,求证:
,求证: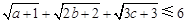 .
. ,且
,且 ,求证:
,求证:
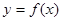 的定义域为
的定义域为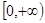 ,且对于任意
,且对于任意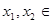
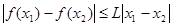 均成立。
均成立。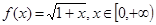 ,求正实数L的取值范围;
,求正实数L的取值范围;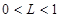 时,正项数列{
时,正项数列{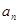 }满足
}满足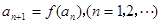
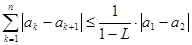 ;
;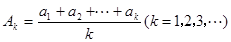 ,求证:
,求证: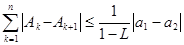 .
.