题目内容
求函数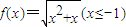 的反函数.
的反函数.
【答案】分析:欲求原函数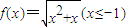 的反函数,即从原函数式中反解出x,后再进行x,y互换,即得反函数的解析式.
的反函数,即从原函数式中反解出x,后再进行x,y互换,即得反函数的解析式.
解答:解:由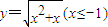
得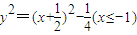 ,
,
∴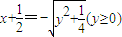 ,
,
∴所求函数的反函数为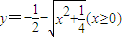 .
.
点评:本题考查反函数的求法,属于基础题目,要会求一些简单函数的反函数,掌握互为反函数的函数图象间的关系.
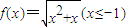 的反函数,即从原函数式中反解出x,后再进行x,y互换,即得反函数的解析式.
的反函数,即从原函数式中反解出x,后再进行x,y互换,即得反函数的解析式.解答:解:由
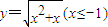
得
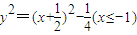 ,
,∴
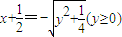 ,
,∴所求函数的反函数为
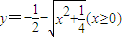 .
.点评:本题考查反函数的求法,属于基础题目,要会求一些简单函数的反函数,掌握互为反函数的函数图象间的关系.

练习册系列答案
相关题目
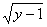 的反函数.
的反函数. .
.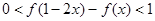 ,求
,求 的取值范围;(6分)
的取值范围;(6分) 是以2为周期的偶函数,且当
是以2为周期的偶函数,且当 时,有
时,有 ,求函数
,求函数
 的反函数.(8分)
的反函数.(8分) .
. ,求
,求 的取值范围;(6分)
的取值范围;(6分) 是以2为周期的偶函数,且当
是以2为周期的偶函数,且当 时,有
时,有 ,求函数
,求函数
 的反函数.(8分)
的反函数.(8分)