��Ŀ����
����С������12�֣����������ʵء���С��ȫ��ͬ��4����ŷֱ�Ϊ1��2��3��4���ס���������һ����Ϸ����������һ�����±�ţ��Żغ�������һ�����±�ţ���������ŵĺ�Ϊ�������Ӯ����������Ӯ���ǻ����¼�Ϊ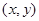 ������
������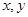 �ֱ�Ϊ�ס�����������ı�š�
�ֱ�Ϊ�ס�����������ı�š�
��1���оٳ����еĻ����¼��������Ӯ�ұ�ŵĺ�Ϊ5���¼������ĸ��ʣ�
��2���Ƚϼ�ʤ�ĸ�������ʤ�ĸ��ʣ���˵��������Ϸ�����Ƿ�ƽ��������ϸ�����̣������֣�
��3�� ��������������ĺ���֮�ͣ������н�����ʲô���Ŀ����Դ�˵�����ɣ�
1������16���ȿ����¼��о����£�1,1������1,2������1,3����(1,4),(2,1),(2,2),(2,3),(2,4)
 (3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)
(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)
2��������Ϸ��ƽ
3����5�Ŀ����Դ�
���������⣺��1������16���ȿ����¼��о����£�1,1������1,2������1,3����(1,4),(2,1),(2,2),(2,3),(2,4)
(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4). ������2��
���ʤ��������֮��Ϊ5Ϊ�¼�A,���¼�A����(1,4)��(2,3) ,(3,2), (4,1) ��4�������¼�������4��
��P(A)=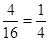 ������4��
������4��
��2��������Ϸ��ƽ��
���ʤΪ�¼�B��ʤΪ�¼�C�����ʤ������1,2����(1,4),
(2,1), (2,3), (3,2), (3,4), (4,1),
(4,3) ��8�������¼������ʤ�ĸ���P(B)=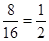 ������6��
������6��
�Ӷ���ʤ�ĸ���P(C)=1- P(B)= 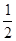 ��
��
��P(B)= P(C) ��������Ϸ��ƽ��������8��
��2���ǡ����������������֮��Ϊ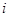 ��Ϊ�¼�
��Ϊ�¼�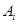 ��
��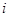 =2��3��4��5��6��7��8��������10��
=2��3��4��5��6��7��8��������10��
�ɣ�1���п�֪�¼�A2�Ļ������Ϊ1�֣��¼�A3�Ļ������Ϊ2�֣��¼�A4�Ļ������Ϊ3�֣��¼�A5�Ļ������Ϊ4�֣��¼�A6�Ļ������Ϊ3�֣�A7�Ļ������Ϊ2�֣�A8�Ļ������Ϊ1�֣��������������������֮��Ϊ5�ĸ������
�𣺲�5�Ŀ����Դ� ������12��
