题目内容
已知圆 与圆
与圆 ,以圆
,以圆 的圆心分别为左右焦点的椭圆
的圆心分别为左右焦点的椭圆 经过两圆的交点.
经过两圆的交点.
(1)求椭圆 的方程;
的方程;
(2)直线 上有两点
上有两点 (
( 在第一象限)满足
在第一象限)满足 ,直线
,直线 与
与 交于点
交于点 ,当
,当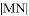 最小时,求线段
最小时,求线段 的长.
的长.
练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
题目内容
已知圆 与圆
与圆 ,以圆
,以圆 的圆心分别为左右焦点的椭圆
的圆心分别为左右焦点的椭圆 经过两圆的交点.
经过两圆的交点.
(1)求椭圆 的方程;
的方程;
(2)直线 上有两点
上有两点 (
( 在第一象限)满足
在第一象限)满足 ,直线
,直线 与
与 交于点
交于点 ,当
,当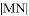 最小时,求线段
最小时,求线段 的长.
的长.
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案