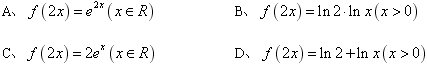题目内容
对任意的x1＜0＜x2，若函数f（x）=a|x-x1|+b|x-x2|的大致图象为如图所示的一条折线（两侧的射线均平行于x轴），试写出a、b应满足的条件______．
当x≤x1时，f（x）=-a（x-x1）-b（x-x2）=-（a+b）x+（ax1+bx2） 由图可知
当x1＜0＜x2时，f（x）=a（x-x1）-b（x-x2）=（a-b）x-ax1+bx2 由图可知
②′
当x≥x2时，f（x）=a（x-x1）+b（x-x2）=（a+b）x-（ax1+bx2）由图又可得出①②两式．
由 ①，①′两式可得a=-b＞0，同时使得②，②′成立．
故答案为：a＞0且a+b=0 （或a=-b＞0）
|
当x1＜0＜x2时，f（x）=a（x-x1）-b（x-x2）=（a-b）x-ax1+bx2 由图可知
|
当x≥x2时，f（x）=a（x-x1）+b（x-x2）=（a+b）x-（ax1+bx2）由图又可得出①②两式．
由 ①，①′两式可得a=-b＞0，同时使得②，②′成立．
故答案为：a＞0且a+b=0 （或a=-b＞0）
练习册系列答案
全优点练单元计划系列答案
相关题目
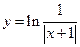的大致图象为（ ）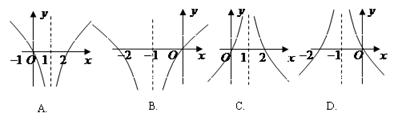
在曲线
上，点Q在曲线
上，则
最小值为（ ）
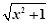（x≤－1），则f－1（2）＝ ．
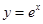的图象与函数
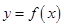的图象关于直线
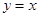对称，则