题目内容
18.直线y=x与曲线C:$\left\{{\begin{array}{l}{x=3cosθ}\\{y=4sinθ}\end{array}}$(θ为参数,π≤θ≤2π)的交点坐标是$(-\frac{12}{5},-\frac{12}{5})$.分析 本题由曲线C的参数方程消去参数后,得到其普通方程,再用两方程联列方程组,得到交点坐标,即本题结论.解题时要注意纵坐标的取值范围.
解答 解:由曲线C:$\left\{{\begin{array}{l}{x=3cosθ}\\{y=4sinθ}\end{array}}$(θ为参数,π≤θ≤2π),
得到:$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{16}=1$(y≤0).
由$\left\{\begin{array}{l}{\frac{{x}^{2}}{9}+\frac{{y}^{2}}{16}=1}\\{y=x}\end{array}\right.$,
得到${y}^{2}=\frac{9×16}{25}$,
∵y≤0,
∴$y=-\frac{12}{5}$,
∴$x=-\frac{12}{5}$.
∴直线y=x与曲线C:$\left\{{\begin{array}{l}{x=3cosθ}\\{y=4sinθ}\end{array}}$(θ为参数,π≤θ≤2π)的交点坐标是$({-\frac{12}{5},-\frac{12}{5}})$.
故答案为:$(-\frac{12}{5},-\frac{12}{5})$.
点评 本题考查了将曲线的参数方程转化为普通方程,本题难度不大,属于基础题.

练习册系列答案
相关题目
10.已知角α的终边落在x轴的正半轴上,则角$\frac{α}{2}$的终边落在( )
| A. | x轴正半轴上 | B. | x轴上 | C. | y轴正半轴上 | D. | y轴上 |
13.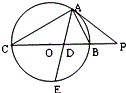 如图,△ABC内接于直径为BC的圆O,过点A作圆O的切线交CB的延长线于点P,∠BAC的平分线分别交BC和圆O于点D、E,若PA=2PB=10.
如图,△ABC内接于直径为BC的圆O,过点A作圆O的切线交CB的延长线于点P,∠BAC的平分线分别交BC和圆O于点D、E,若PA=2PB=10.
(1)求证:AC=2AB;
(2)求AD•DE的值.
 如图,△ABC内接于直径为BC的圆O,过点A作圆O的切线交CB的延长线于点P,∠BAC的平分线分别交BC和圆O于点D、E,若PA=2PB=10.
如图,△ABC内接于直径为BC的圆O,过点A作圆O的切线交CB的延长线于点P,∠BAC的平分线分别交BC和圆O于点D、E,若PA=2PB=10.(1)求证:AC=2AB;
(2)求AD•DE的值.
3.已知集合A={1,2,3},B={Z∈Z|1<x<4},则A∩B=( )
| A. | {1} | B. | {2,4} | C. | {2,3} | D. | (1,4) |
10.已知f(x)=xlnx-ax,g(x)=x3-x+6,若对任意的x∈(0,+∞),2f (x)≤g′(x)+2恒成立,则实数a的取值范围为( )
| A. | [-2,-$\frac{1}{3}$] | B. | [-2,+∞) | C. | (-∞,-$\frac{1}{3}$] | D. | (-∞,-2] |
 为了解某地高中生身高情况,研究小组在该地高中生中随机抽取30名高中生的身高编成如图所示的茎叶图(单位:cm);若身高在175cm以上(包括175cm)定义为“高个子”,身高在175以下(不包括175cm)定义为“非高个子”.
为了解某地高中生身高情况,研究小组在该地高中生中随机抽取30名高中生的身高编成如图所示的茎叶图(单位:cm);若身高在175cm以上(包括175cm)定义为“高个子”,身高在175以下(不包括175cm)定义为“非高个子”.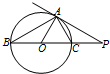 如图,已知PA是圆O的切线,切点为A,直线PO交圆O于B,C两点,AC=1,∠BAP=120°,则圆O的面积为π.
如图,已知PA是圆O的切线,切点为A,直线PO交圆O于B,C两点,AC=1,∠BAP=120°,则圆O的面积为π.