题目内容
如图甲,⊙O的直径AB=2,圆上两点C、D在直径AB的两侧,且∠CAB= ,∠DAB=
,∠DAB= .沿直径AB折起,使两个半圆所在的平面互相垂直(如图乙),F为BC的中点,E为AO的中点.根据图乙解答下列各题:
.沿直径AB折起,使两个半圆所在的平面互相垂直(如图乙),F为BC的中点,E为AO的中点.根据图乙解答下列各题:

(1)求三棱锥C-BOD的体积;
(2)求证:CB⊥DE;
(3)在 上是否存在一点G,使得FG∥平面ACD?若存在,试确定点G的位置;若不存在,请说明理由.
上是否存在一点G,使得FG∥平面ACD?若存在,试确定点G的位置;若不存在,请说明理由.
(1)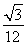 (2)见解析(3)G为
(2)见解析(3)G为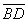 的中点
的中点
【解析】(1)∵C为圆周上一点,且AB为直径,∴∠C=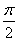 ,
,
∵∠CAB=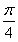 ,∴AC=BC,
,∴AC=BC,
∵O为AB的中点,∴CO⊥AB,
∵AB=2,∴CO=1.
∵两个半圆所在平面ACB与平面ADB互相垂直且其交线为AB,
∴CO⊥平面ABD,∴CO⊥平面BOD.
∴CO就是点C到平面BOD的距离,
S△BOD=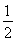 S△ABD=
S△ABD=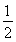 ×
×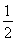 ×1×
×1×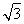 =
=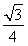 ,
,
∴VC-BOD=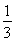 S△BOD·CO=
S△BOD·CO=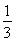 ×
×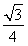 ×1=
×1=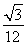 .
.
(2)证明:在△AOD中,∵∠OAD=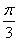 ,OA=OD,
,OA=OD,
∴△AOD为正三角形,
又∵E为OA的中点,∴DE⊥AO,
∵两个半圆所在平面ACB与平面ADB互相垂直且其交线为AB,
∴DE⊥平面ABC.
又CB?平面ABC,∴CB⊥DE.
(3)存在满足题意的点G,G为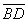 的中点.证明如下:
的中点.证明如下:
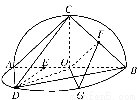
连接OG,OF,FG,
易知OG⊥BD,
∵AB为⊙O的直径,
∴AD⊥BD,
∴OG∥AD,
∵OG?平面ACD,AD?平面ACD,
∴OG∥平面ACD.
在△ABC中,O,F分别为AB,BC的中点,
∴OF∥AC,
∴OF∥平面ACD,
∵OG∩OF=O,
∴平面OFG∥平面ACD.
又FG?平面OFG,∴FG∥平面ACD.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目












