题目内容
已知函数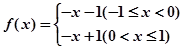 ,则
,则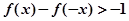 的解集为( )
的解集为( )
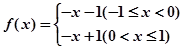 ,则
,则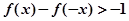 的解集为( )
的解集为( )A.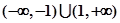 | B.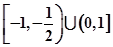 |
C.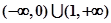 | D.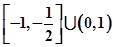 |
B
已知f(x)为分段函数,要求f(x)-f(-x)>-1的解集,就必须对其进行讨论:①若-1≤x<0时;②若x=0,③若0<x≤1,进行求解;
解:∵f(x)=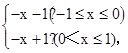
∴①若-1≤x<0时,也即0<-x≤1,
∴f(x)-f(-x)=-x-1-(x+1)>-1,解得x<-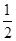 ,
,
∴-1<x<-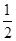
②若x=0,则f(0)=-1,∴f(x)-f(-x)=-1,故x≠0;
③若0<x≤1,则-1≤-x<0,∴-x+1-(x-1)>-1,
x< ,
,
∴0<x≤1;
综上①②得不等式解集为:[-1,-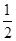 )∪(0,1];
)∪(0,1];
故选B;
解:∵f(x)=
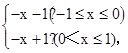
∴①若-1≤x<0时,也即0<-x≤1,
∴f(x)-f(-x)=-x-1-(x+1)>-1,解得x<-
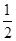 ,
,∴-1<x<-
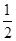
②若x=0,则f(0)=-1,∴f(x)-f(-x)=-1,故x≠0;
③若0<x≤1,则-1≤-x<0,∴-x+1-(x-1)>-1,
x<
 ,
,∴0<x≤1;
综上①②得不等式解集为:[-1,-
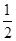 )∪(0,1];
)∪(0,1];故选B;

练习册系列答案
相关题目
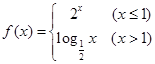 ,则函数
,则函数 的图象是 ( )
的图象是 ( )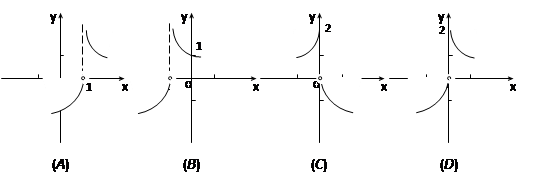
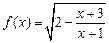 的定义域为A,不等式
的定义域为A,不等式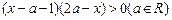 的解集为B.
的解集为B.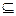 A,求实数a的取值范围.
A,求实数a的取值范围.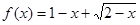 的值域为( )
的值域为( )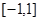
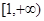
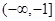
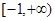
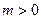 ,
,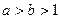 ,
,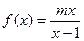 ,比较
,比较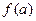 与
与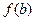 的大小。
的大小。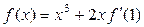 ,则
,则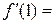 .
. 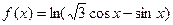 的定义域为____________
的定义域为____________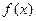 是定义在R上周期为3的奇函数,若
是定义在R上周期为3的奇函数,若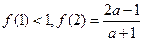 ,则有
,则有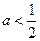 且
且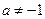
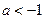 或
或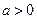

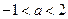
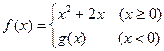 为奇函数,则
为奇函数,则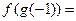 ______________.
______________.