题目内容
【题目】已知函数![]()
![]() .
.
(Ⅰ)当![]() 时,求
时,求![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(Ⅱ)若函数![]() 与
与![]() 图象在
图象在![]() 上有两个不同的交点,求实数
上有两个不同的交点,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)y=2x-1. (Ⅱ)[![]() ].
].
【解析】【试题分析】(I)当![]() 时,求出
时,求出![]() 和
和![]() 的值,利用点斜式求得切线方程.(II)令
的值,利用点斜式求得切线方程.(II)令![]() ,化简得
,化简得![]() ,构造函数
,构造函数![]() ,利用导数求得
,利用导数求得![]() 在区间
在区间![]() 上的极大值为
上的极大值为![]() ,通过计算
,通过计算![]() 和
和![]() 可知
可知![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,由此可用最大值大于零,最小值不大于零列不等式组,求得
,由此可用最大值大于零,最小值不大于零列不等式组,求得![]() 的取值范围.
的取值范围.
【试题解析】
(Ⅰ)解 当![]() 时,f(x)=2lnx-x2+2x,f′(x)=
时,f(x)=2lnx-x2+2x,f′(x)=![]() -2x+2,
-2x+2,
切点坐标为(1,1),切线的斜率k=f′(1)=2,
则切线方程为y-1=2(x-1),即y=2x-1.
(Ⅱ)解:由题意可得:2lnx-x2+m=0,令h(x)=2lnx-x2+m,
则h′(x)=![]() -2x=
-2x=![]() ,
,
∵x∈![]() ,故h′(x)=0时,x=1.
,故h′(x)=0时,x=1.
当![]() <x<1时,h′(x)>0;当1<x<e时,h′(x)<0.
<x<1时,h′(x)>0;当1<x<e时,h′(x)<0.
故h(x)在x=1处取得极大值h(1)=m-1.
又![]() =m-2-
=m-2-![]() ,h(e)=m+2-e2,h(e)-
,h(e)=m+2-e2,h(e)-![]() =4-e2+
=4-e2+![]() <0,
<0,
则h(e)<![]() ,
,
∴h(x)在[![]() ]上的最小值为h(e).
]上的最小值为h(e).
h(x)在[![]() ]上有两个零点的条件是
]上有两个零点的条件是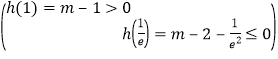 ,
,
解得1<m≤2+![]()
∴实数m的取值范围是[![]() ].
].

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
【题目】中国的钨矿资源储量丰富,在全球已经探明的钨矿产资源储量中占比近![]() ,居全球首位。中国又属赣州钨矿资源最为丰富,其素有“世界钨都”之称。某科研单位在研发的钨合金产品的过程中发现了一种新合金材料,由大数据测得该产品的性能指标值与这种新合金材料的含量x(单位:克)的关系为:当
,居全球首位。中国又属赣州钨矿资源最为丰富,其素有“世界钨都”之称。某科研单位在研发的钨合金产品的过程中发现了一种新合金材料,由大数据测得该产品的性能指标值与这种新合金材料的含量x(单位:克)的关系为:当![]() 时,
时, ![]() 是
是![]() 的二次函数;当
的二次函数;当![]() 时,
时, ![]() .测得部分数据如表.
.测得部分数据如表.
x(单位:克) | 0 | 1 | 2 | 9 | … |
y | 0 |
| 3 |
| … |
(1)求y关于x的函数关系式y=![]()
(2)求函数![]() 的最大值
的最大值


