Question

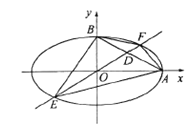
【题目】如图，已知椭圆，点是它的两个顶点，过原点且斜率为的直线与线段相交于点，且与椭圆相交于两点．

（1）若，求的值；

（2）求四边形面积的最大值．

Answer 1

【答案】（1）或；（2）．

【解析】

试题（1）先由两点式求得直线的方程，然后设的方程为.设，，，联立直线与椭圆的方程，得到间的关系，再由与点在线段上求得的值；（2）由点到直线的距离公式分别求得点到线段的距离，从而得到四边形的面积的表面式，进而求得其最大值．

试题解析：（1）依题设得椭圆的顶点，则直线的方程为.

设直线的方程为.设，其中，

联立直线与椭圆的方程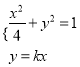，消去，得方程.（3分）

故，由知，，

得，由点在线段上，知，得，

所以，化简，得，解得或.

（2）根据点到直线的距离公式，知点到线段的距离分别为，

又，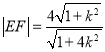

所以四边形的面积为

，

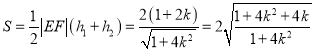
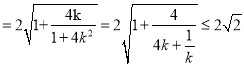当且仅当，即时，取等号，

所以四边形面积的最大值为.